Study the information carefully to answer the question that follow:
There are 12500 graduates (male + female) in a district who are preparing for various competitive examinations. 90% of these graduates apply for separate exams for recruitment into Railways, Bank and SSC. The respective ratio of number of applicants for only one exam, two exams and all the three exams is:16:20:9. Of those who applied, for only one exam, 12% applied for railways, 26%.for Banks and the remaining for -SSC. The respective male to female ratios of those applying for only Railways, only Banks and only. SSC are 7:5,8:5 and 9:7 respectively. The total number of applicants for both Railways & Banks and for both Railways &. SSC taken together equals that for both Banks & SSC. The number of applicants for both Railways & SSC exceeds that for both Railways and banks by 100.60% of those applying for both bank & SSC are females. The number of males applying for both Railways &SSC is 20% more than for both Railways & Banks which in turn is half of that for both Bank & SSC. The, number of female applicants who applied for all the three exams is 665.
The number of male applicants applying- for only two exams is what per cent of total number of male applicants?
35%
42%
45%
48%
The correct Answer is:A
To solve the problem step by step, we will break down the information provided and calculate the required values systematically.
Step 1: Calculate the total number of applicants
Given that 90% of 12,500 graduates applied for the exams:
Total applicants=0.90×12500=11250
Step 2: Determine the ratio of applicants for one exam, two exams, and all three exams
The ratio of applicants for only one exam, two exams, and all three exams is given as 16:20:9. Let the common multiplier be x.
Applicants for one exam=16x,for two exams=20x,for all three exams=9x
The total applicants can be expressed as:
16x+20x+9x=11250⟹45x=11250⟹x=1125045=250
Step 3: Calculate the number of applicants for each category
Using x=250:
- Applicants for only one exam:
16x=16×250=4000
- Applicants for two exams:
20x=20×250=5000
- Applicants for all three exams:
9x=9×250=2250
Step 4: Determine the distribution of applicants for only one exam
- For Railways (12% of 4000):
Railways=0.12×4000=480
- For Banks (26% of 4000):
Banks=0.26×4000=1040
- For SSC (remaining):
SSC=4000−(480+1040)=4000−1520=2480
Step 5: Calculate the male to female ratios for each category
- For Railways (7:5):
Total for Railways=480⟹Males=712×480=280,Females=480−280=200
- For Banks (8:5):
Total for Banks=1040⟹Males=813×1040=640,Females=1040−640=400
- For SSC (9:7):
Total for SSC=2480⟹Males=916×2480=1395,Females=2480−1395=1085
Step 6: Set up equations for applicants for two exams
Let a be the number of applicants for both Railways & Banks, b for Railways & SSC, and c for Banks & SSC. We know:
b=a+100
a+b+c=5000
Substituting b:
a+(a+100)+c=5000⟹2a+c+100=5000⟹2a+c=4900(1)
Step 7: Set up another equation using the total for two exams
From the problem, we know:
b+c=a+100+c=4900−a
This gives us:
c=4900−2a(2)
Step 8: Solve for a, b, and c
From equation (1) and substituting (2) into it:
2a+(4900−2a)=4900⟹4900=4900
This means we need more information to solve for a, b, and c.
Step 9: Calculate male applicants for both Railways & SSC
Given that males applying for both Railways & SSC is 20% more than for both Railways & Banks, which is half of that for both Banks & SSC. Let m be the males for Railways & Banks:
Males for Railways & SSC=m+0.2m=1.2m
m=12×Males for Banks & SSC
Step 10: Calculate total male applicants
Finally, the total male applicants can be calculated by summing the males from all categories:
Total males=280+640+1395+Males for two exams
Step 11: Calculate percentage of males applying for only two exams
Let’s say the total males who applied for only two exams is M:
Percentage=(MTotal males)×100
Conclusion
After calculating all the values, we can find the required percentage of male applicants applying for only two exams.
Given that 90% of 12,500 graduates applied for the exams:
Total applicants=0.90×12500=11250
The ratio of applicants for only one exam, two exams, and all three exams is given as 16:20:9. Let the common multiplier be x.
Applicants for one exam=16x,for two exams=20x,for all three exams=9x
The total applicants can be expressed as:
16x+20x+9x=11250⟹45x=11250⟹x=1125045=250
Using x=250:
- Applicants for only one exam:
16x=16×250=4000
- Applicants for two exams:
20x=20×250=5000
- Applicants for all three exams:
9x=9×250=2250
- For Railways (12% of 4000):
Railways=0.12×4000=480
- For Banks (26% of 4000):
Banks=0.26×4000=1040
- For SSC (remaining):
SSC=4000−(480+1040)=4000−1520=2480
- For Railways (7:5):
Total for Railways=480⟹Males=712×480=280,Females=480−280=200
- For Banks (8:5):
Total for Banks=1040⟹Males=813×1040=640,Females=1040−640=400
- For SSC (9:7):
Total for SSC=2480⟹Males=916×2480=1395,Females=2480−1395=1085
Let a be the number of applicants for both Railways & Banks, b for Railways & SSC, and c for Banks & SSC. We know:
b=a+100
a+b+c=5000
Substituting b:
a+(a+100)+c=5000⟹2a+c+100=5000⟹2a+c=4900(1)
From the problem, we know:
b+c=a+100+c=4900−a
This gives us:
c=4900−2a(2)
From equation (1) and substituting (2) into it:
2a+(4900−2a)=4900⟹4900=4900
This means we need more information to solve for a, b, and c.
Given that males applying for both Railways & SSC is 20% more than for both Railways & Banks, which is half of that for both Banks & SSC. Let m be the males for Railways & Banks:
Males for Railways & SSC=m+0.2m=1.2m
m=12×Males for Banks & SSC
Finally, the total male applicants can be calculated by summing the males from all categories:
Total males=280+640+1395+Males for two exams
Let’s say the total males who applied for only two exams is M:
Percentage=(MTotal males)×100
After calculating all the values, we can find the required percentage of male applicants applying for only two exams.
Similar Questions
Knowledge Check
Read the information given below and answer the questions that follow:
Following table gives the data on the number of students who appeared, qualified and were selected from various states in a national level exam.
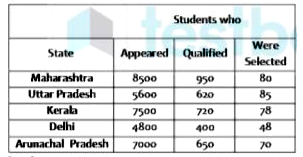
What percentage of students who appeared in the exam were selected?A1.08%B0.90%C1.2%D2.11%The table given below shows the number of applicants who have applied for exam at various centres as percentage of total number of applicants. The table also shows the number online applicants and absent applicants as a percentage of total applicants of each centre. Total number of applicants is 1200000.
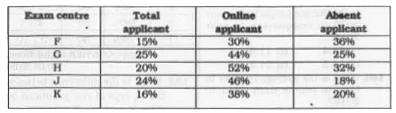
If A equals to 15% of total applicants who are present at exam centre F and B equals to present applicants at exam centre K, then A is what per cent of B?A(a) 18.18B(b) 11.25C(c) 13.33D(d) 14.28The table given below shows the number of applicants who have applied for exam at various centres as percentage of total number of applicants. The table also shows the number online applicants and absent applicants as a percentage of total applicants of each centre. Total number of applicants is 1200000.

What is the ratio of total number of present applicants from exam centre K to total number of offline applicants from exam centre J?A40:41B80:81C10:9D7:11
The table given below shows the number of applicants who have applied for exam at various centres as percentage of total number of applicants. The table also shows the number online applicants and absent applicants as a percentage of total applicants of each centre. Total number of applicants is 1200000.

Total number of offline applicants from exam centre H, K and F are how much less than the total number of present applicants from exam centre G and J?
View SolutionThe given pie chart shows the stream wise distribution (in degrees) of the candidates who applied for an entrance exam. The total number of candidates who applied was 720000 and out of which 5400 have qualified the exam
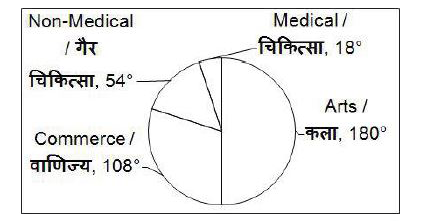
What percentage of the total candidates belong the non-medical?
View SolutionThe given pie chart shows the stream wise distribution (in degrees) of the candidates who applied for an entrance exam. The total number of candidates who applied was 720000 and out of which 5400 have qualified the exam
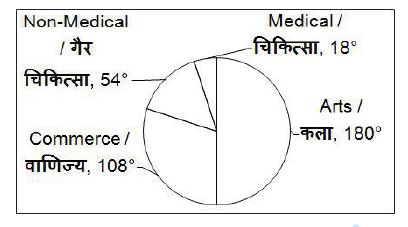
What percentage of the total candidates who applied for the exams have qualified it?
View SolutionIn a team there are 240 members (males and females). Two-third of them are males. Fifteen percent of males are graduates. Remaining males are non-graduates. Three-fourth of the females are graduates. Remaining females are non-graduates.
What is the sum of the number of females who are graduates and the number of males who are non- graduates ?
View SolutionIn a team there are 240 members (males and females). Two-third of them are males. Fifteen percent of males are graduates. Remaining males are non-graduates. Three-fourth of the females are graduates. Remaining females are non-graduates.
What is the difference between the number of females whos are non-graduates and the number of males who are graduates ?
View Solution
