Case Study-2 : Read the above paragraph and answer the following questions.
In a morning walk, Naveeka, Arjun and Vedant step off together, their steps measuring 240 cm, 90 cm, 120 cm respectively. They want to go for a juice shop for a health issue, which is situated near by them.
A largest positive integer that divides given two positive integers is called:
HCF
LCM
co-prime
None of these
The correct Answer is:A
To solve the question, we need to identify the largest positive integer that divides the given step lengths of Naveeka, Arjun, and Vedant, which are 240 cm, 90 cm, and 120 cm respectively. This integer is known as the Highest Common Factor (HCF) or Greatest Common Divisor (GCD).
1. Identify the Numbers:
The step lengths of Naveeka, Arjun, and Vedant are:
- Naveeka: 240 cm
- Arjun: 90 cm
- Vedant: 120 cm
2. Find the Prime Factorization of Each Number:
- For 240:
- 240 = 2 × 120
- 120 = 2 × 60
- 60 = 2 × 30
- 30 = 2 × 15
- 15 = 3 × 5
- Therefore, 240 = 2^4 × 3^1 × 5^1
- For 90:
- 90 = 2 × 45
- 45 = 3 × 15
- 15 = 3 × 5
- Therefore, 90 = 2^1 × 3^2 × 5^1
- For 120:
- 120 = 2 × 60
- 60 = 2 × 30
- 30 = 2 × 15
- 15 = 3 × 5
- Therefore, 120 = 2^3 × 3^1 × 5^1
3. Identify the Common Factors:
Now we will identify the common prime factors from the factorizations:
- 240: 2^4, 3^1, 5^1
- 90: 2^1, 3^2, 5^1
- 120: 2^3, 3^1, 5^1
The common prime factors are:
- For 2: the minimum power is 2^1 (from 90)
- For 3: the minimum power is 3^1 (from both 240 and 120)
- For 5: the minimum power is 5^1 (common in all)
4. Calculate the HCF:
Now, we multiply the common factors with their minimum powers:
HCF = 2^1 × 3^1 × 5^1 = 2 × 3 × 5 = 30
5. Conclusion:
The largest positive integer that divides the step lengths of Naveeka, Arjun, and Vedant is 30 cm.
The step lengths of Naveeka, Arjun, and Vedant are:
- Naveeka: 240 cm
- Arjun: 90 cm
- Vedant: 120 cm
- For 240:
- 240 = 2 × 120
- 120 = 2 × 60
- 60 = 2 × 30
- 30 = 2 × 15
- 15 = 3 × 5
- Therefore, 240 = 2^4 × 3^1 × 5^1
- 90 = 2 × 45
- 45 = 3 × 15
- 15 = 3 × 5
- Therefore, 90 = 2^1 × 3^2 × 5^1
- 120 = 2 × 60
- 60 = 2 × 30
- 30 = 2 × 15
- 15 = 3 × 5
- Therefore, 120 = 2^3 × 3^1 × 5^1
Now we will identify the common prime factors from the factorizations:
- 240: 2^4, 3^1, 5^1
- 90: 2^1, 3^2, 5^1
- 120: 2^3, 3^1, 5^1
- For 2: the minimum power is 2^1 (from 90)
- For 3: the minimum power is 3^1 (from both 240 and 120)
- For 5: the minimum power is 5^1 (common in all)
Now, we multiply the common factors with their minimum powers:
HCF = 2^1 × 3^1 × 5^1 = 2 × 3 × 5 = 30
The largest positive integer that divides the step lengths of Naveeka, Arjun, and Vedant is 30 cm.
Topper's Solved these Questions
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section - A
6 Videos
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section - B
5 Videos
- SAMPLE PAPER 5BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - Section -C
2 Videos
- SAMPLE PAPER 7BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - Section -C
7 Videos
Similar Questions
Two linear parallel conductors carrying currents in the same direction attract each other and two linear parallel conductors carrying currents in opposite direction repel each other. The force acting per unit length due to currents I1 and I2 in two linear parallel conductors held distance r apart in vacuum in SI unit is F=μ04π2I1I2r
Read the above passage and answer the following questions:
(i) What is the basic reason for the force between two linear parallel conductors carrying currents?
(ii) Two straight wires A and B of lengths 2cm and 20cm, carrying currents 2⋅0A and 5⋅0A respectively in opposite directions are lying parallel to each other 4⋅0cm apart. The wire A is held near the middle of wire B. What is the force on 20cm long wire B?
(iii) What does this study imply in day to day life?
View SolutionWhen an electric dipole of moment |→p|=q×2a is held at an angle θ, with the direction of uniform external electric field →E, a torque τ=pEsinθ acts on the dipole. This torque tries to align the electric dipole in the direction of the field. When →p is along →E,θ∘,τ=pEsin0∘=zero. The dipole is in stabel equilibrium. The energy possessed by the dipole by virtue of its particular position in the electric field is called potential energy of dipole.
U=W=−pE(cosθ2−cosθ1)
θ1=90∘ is the position of zero potential energy.
∴U=W=−pE(cosθ−cos90∘)=−pEcosθ.
For stable equillibrium, θ0∘,∴U=−pE = minimum.
Read the above passage and answer the following questions :
(i) What is the direction of torque acting on electric dipole held at an angle with uniform external electric field ?
(ii) An electric dipole of length 10cm having charges ±6×10−3C, placed at 30∘ with respect to a uniform electric field experiences a torque of magnitude 6√3N−m. Calculate.
(a) magnitude of electric field. (b) potential energy of dipole.
(iii) What is the physical significance of this concept in our day to day life ?
View Solution
Knowledge Check
Attempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
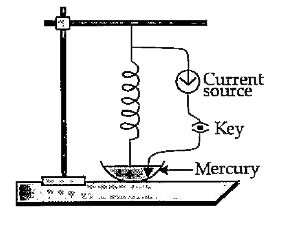
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Why the spring shrinks in Roget's spiral?
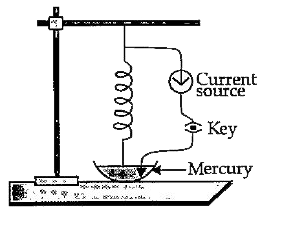 AThe spring functions as a solenoidBDue to force acting between two current carrying wiresCDue to magnetic effect of currentDSince the spring is soft
AThe spring functions as a solenoidBDue to force acting between two current carrying wiresCDue to magnetic effect of currentDSince the spring is softAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What else can be used instead of mercury in Roget's spiral?
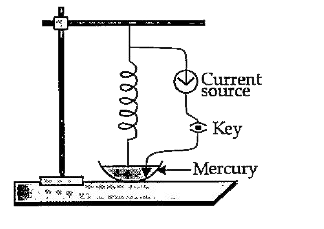 AAny liquidBWaterCKerosene oilDOnly mercury, nothing else
AAny liquidBWaterCKerosene oilDOnly mercury, nothing elseAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What are main 3 components in a Roget's spiral?
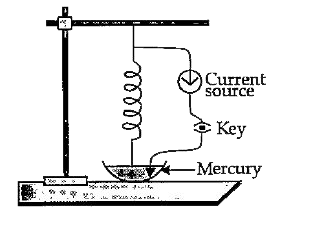 AMarcury, AC voltage sourceBMercury, DC voltage sourceCMercury, DC voltage source, keyDMercury, AC voltage source, key
AMarcury, AC voltage sourceBMercury, DC voltage sourceCMercury, DC voltage source, keyDMercury, AC voltage source, key
A rectangular coil of n turns each of area A, carrying current I, when suspended in a uniform magnetic field B, experiences a torque
τ=nIBAsinθ
where θ is the angle with a normal drawn on the plane of coil makes with the direction of magnetic field. This torque tends to rotate the coil and bring it in equilibrium position. In stable equilibrium state, the resultant force on the coil is zero. The torque on coil is also zero and the coil has minimum potential energy.
Read the above passage and answer the following questions:
(i) In which position, a current carrying coil suspended in a uniform magnetic field experiences (a) minimum torque and (b) maximum torque?
(ii) A circular coil of 200 turns, radius 5cm carries a current of 2⋅0A. It is suspended vertically in a uniform horizontal magnetic field of 0⋅20T, with the plane of the coil making an angle of 60∘ with the field lines. Calculate the magnitude of the torque that must be applied on it to prevent it from turning.
(iii) What is the basic value displayed by the above study?
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Magnetic effects:
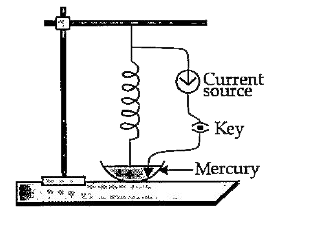
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
The force 10−3 N, is equivalent to:
View SolutionRead the passage given below and answer the questions that follow :
The difference in the ways of thinking and perception in the people of two different generations, which results in behavioural differences and sometimes conflict among them, is usually called generation gap. Generation gap is generally seen in the family between parents and their children. It is not only because of the gap in age, but also because of the way parents react to a particular situation. Children being very young and immature do not understand the way of thinking of their parents. In many cases, the parents, even if they are matured, do not empathize with the changing values and thinking pattern of the modern world. This creates a communication gap between these two generations.
Generation gap between parents and children is mostly caused by parents themselves. They do not talk openly to their children and do not take part in solving their problems. This behaviour gives the impression about parents being authoritative persons, because they only dictate without understanding the problems faced by their children. As a result, the children become mentally isolated from their parents. Some parents become so busy with their work that they don't spend quality time with their families, which makes them completely unaware of how their children are growing, what kind of mentality is being developed in them, and so on. This ultimately creates a gap between them. They only realize it when it is too late.
Changes in technology have led to the generation gap in this modern world. Children tend to spend most of their time with their digital devices and are so busy with social media, that they do not discuss their problems with their parents. The internet provides solutions to most of the worldly problems. So children, instead of contacting their own parents, seek the help of internet in case of any problem, thus again reducing the communication, leading to a generation gap between them. The generation gap has greatly increased these days because the time is changing fast and people find it difficult to cope up with this change. To overcome this problem, parents should show interest in all matters of their children and deal with them positively, instead of just scolding them and leaving them alone to deal with their problems. Giving time to the children, having open communication, and allowing the child to feel free and remain free from pressure, will eventually reduce the generation gap to a tolerable extent.
What is meant by the word, 'particular? (Para 2)
View SolutionRead the given passage carefully and answer the questions that follow. Certain words are printed in bold to help you locate them while answering some of these. Renewable Energy (RE) is the future. With that said, one can argue that the future has arrived, in parts at least. Worldwide acceptance towards green energy is giving the sustainable energy sector more market share every year. The growth is consistent, with each year out-performing the previous, leading renewable energy to account for 1/3rd of global energy capacity.
It’s fair to state that the growth trajectory is incredible, and considering that it took only a little more than a just decade to reach this position, we could call it _____________. However, the most important question is, is this satisfactory? The goal of green energy transition is to solve growing energy scarcity and reduce dependency on fossil fuels in order to move towards a fully sustainable energy landscape. Therefore, to identify success, we need to compare renewable energy growth with the current scenario.
According to WHO’s estimates, currently, more than 7 million people die every year from pollution, up from 4.2 million in 2016. Fossil fuel consumption has increased globally from 94,462/twh in 2000 to 1,33,853/twh now. The rise in population (currently 7.7 billion) indicates a steady growth in energy demand worldwide. In comparison, the fact that renewable energy took a decade to become 1/3 of energy capacity is not the ideal pace, considering we might not have two more decades to wait for RE to catch up.
Which of the following statement (s) if true, will support the author’s claim that the rate of growth in Renewable Energy is not satisfactory?
I. The use of fossil fuels to satisfy energy needs continues to be a popular choice.
II. The issue of energy scarcity is being addressed by the use of RE in a more appropriate manner.
III. Government and private organisations are working together to develop technology which operates on RE.
View Solution
