Case Study-1: Consider a right triangle, where a and b are its length, and base and c is its hypotenuse as shown below. When we observe and apply the trigonometric functions to make a relationship between angles and sides of the right triangle. We can obtain the results as per the calculations and the table depicted below.
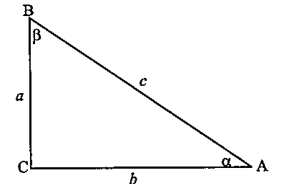
If the right angle of the right triangle ABC is at the point C, then the sine (sin), cosine (cos) and tangent (tan) of the angles α (at the point A) and β (at the point B). It should be noted that sin α cos β are the equal and same goes for sin α and cos β. So, to find sine of the angle, we divided the side that is opposite of that angle and the hypotenuse. To find the cosine of the angle, we divide the side that makes that angle (adjacent side) by the hypotenuse.
Thus,
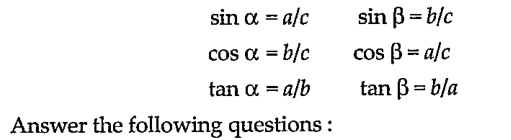
Calculate tanα+tanβ.
25/12
12/25
7/12
12/7
The correct Answer is:A
Step by step video, text & image solution for Case Study-1: Consider a right triangle, where a and b are its length, and base and c is its hypotenuse as shown below. When we observe and apply the trigonometric functions to make a relationship between angles and sides of the right triangle. We can obtain the results as per the calculations and the table depicted below. If the right angle of the right triangle ABC is at the point C, then the sine (sin), cosine (cos) and tangent (tan) of the angles alpha (at the point A) and beta (at the point B). It should be noted that sin alpha cos beta are the equal and same goes for sin alpha and cos beta. So, to find sine of the angle, we divided the side that is opposite of that angle and the hypotenuse. To find the cosine of the angle, we divide the side that makes that angle (adjacent side) by the hypotenuse. Thus, Calculate tanalpha+tanbeta. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 4BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - Section-A
7 Videos
- SAMPLE PAPER 4BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - Section - B
5 Videos
- SAMPLE PAPER 3BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - Section - C
5 Videos
- SAMPLE PAPER 5BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - Section -C
2 Videos
Similar Questions
Knowledge Check
Base of a right angled triangle is
A√(Hypotenous)2+(Perpendicular)2B√(Hypotenous)2−(Perpendicular)2C√(Perpendicular)2−(Hypotenous)2DNone of TheseIf the length of sides of right angled triangle are in AP, then their ratio is
A3:4:5B2:3:4C1:2:3Dnone of theseIn a right-angled triangle with sides a and b, hypotenuse c, the altitude drawn on the hypotenuse is x. Then
Aab=x2B1a+1b=1xCa2+b2=2x2D1a2+1b2=1x2
Show that in a right angled triangle, the hypotenuse is the longest side.
View SolutionConstruct a right angled triangle whose base is 12cm and sum of its hypotenuse and other side is 18cm.
View SolutionABC is right triangle , right angled at A, then tanB⋅tanC=_____
View SolutionThe point where the triangle forms the right angle in the right angled triangle is known as the _______.
View SolutionThe point where the triangle forms the right angle in the right angled triangle is known as the _______.
View Solution