Give the polynomial of degree 2 with sum and product of its zeros as −12 and -3 respectively:
k(x2−x+6)
k(2x2+x−6)
k(x2+x−3)
k(x2−2x+3)
The correct Answer is:B
To find the quadratic polynomial of degree 2 with the given sum and product of its zeros, we can follow these steps:
Step 1: Understand the standard form of a quadratic polynomial
The standard form of a quadratic polynomial is given by:
P(x)=Ax2+Bx+C
where A, B, and C are constants.
Step 2: Use the relationships for the sum and product of zeros
For a quadratic polynomial P(x)=Ax2+Bx+C:
- The sum of the zeros α+β is given by:
α+β=−BA
- The product of the zeros αβ is given by:
αβ=CA
Step 3: Set up equations based on the given values
From the problem, we know:
- The sum of the zeros α+β=−12
- The product of the zeros αβ=−3
Using these values, we can set up the following equations:
1. From the sum:
−BA=−12
This simplifies to:
B=A2
2. From the product:
CA=−3
This simplifies to:
C=−3A
Step 4: Substitute B and C into the polynomial
Now we substitute B and C back into the standard form of the polynomial:
P(x)=Ax2+(A2)x+(−3A)
This can be rewritten as:
P(x)=Ax2+A2x−3A
Step 5: Factor out A
We can factor out A from the polynomial:
P(x)=A(x2+12x−3)
Step 6: Choose a value for A
To simplify, we can choose A=2 (this is a common choice to eliminate fractions):
P(x)=2(x2+12x−3)
This gives us:
P(x)=2x2+x−6
Final Polynomial
Thus, the required quadratic polynomial is:
P(x)=2x2+x−6
The standard form of a quadratic polynomial is given by:
P(x)=Ax2+Bx+C
where A, B, and C are constants.
For a quadratic polynomial P(x)=Ax2+Bx+C:
- The sum of the zeros α+β is given by:
α+β=−BA
- The product of the zeros αβ is given by:
αβ=CA
From the problem, we know:
- The sum of the zeros α+β=−12
- The product of the zeros αβ=−3
1. From the sum:
−BA=−12
This simplifies to:
B=A2
CA=−3
This simplifies to:
C=−3A
Now we substitute B and C back into the standard form of the polynomial:
P(x)=Ax2+(A2)x+(−3A)
This can be rewritten as:
P(x)=Ax2+A2x−3A
We can factor out A from the polynomial:
P(x)=A(x2+12x−3)
To simplify, we can choose A=2 (this is a common choice to eliminate fractions):
P(x)=2(x2+12x−3)
This gives us:
P(x)=2x2+x−6
Thus, the required quadratic polynomial is:
P(x)=2x2+x−6
Topper's Solved these Questions
Similar Questions
Case Study-2:
Radha decorated the door of her house with garlands on the occassion of Diwali. Each garland forms the shape of a parabola as shown in the figure.
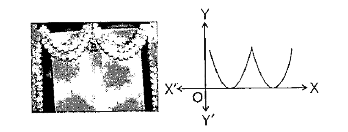
A quadratic polynomial with the sum and product of its zeroes as 1 and -2 respectively, is:
View SolutionRadha decorated the door of her house with garlands on the occassion of Diwali. Each garland forms the shape of a parabola.
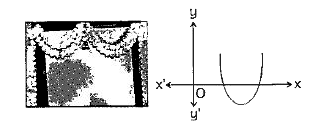
A quadratic polynomial with the sum and product of its zeroes as -1 and -2 respectively, is:
View SolutionFind the polynomial whose sum and product of the zeros are −12 and 12 respectively.
View SolutionFind a quadratic polynomial, the sum and product of whose zeroes are - 3 and 2 respectively.
View SolutionFind the quadratic polynomial, the sum and product of whose zeroes are - 3 and 2 respectively. Hence find the zeroes.
View SolutionFind a quadratic polynomial, the sum and product of whose zeros are −5and6 respectively.
View SolutionFind a quadratic polynomial, the sum and product of whose zeroes are −3and 2, respectively.
View SolutionFind a quadratic polynomial, the sum and product of whose zeros is 4 and 1 respectively.
View SolutionFind the quadratic polynomial sum and product of whose zeroes are -1 and -20 respectively. Also, find the zeroes of the polynomial so obtained
View SolutionFrom a quadratic polynomial, the sum and product of whose zeros are (−3) and 2 respectivily.
View Solution
