The area of the triangle in the given figure (in sq. units) is:

15
10
7.5
2.5
The correct Answer is:C
Step by step video, text & image solution for The area of the triangle in the given figure (in sq. units) is: by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 4BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - Section-A
7 Videos
- SAMPLE PAPER 4BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - Section - B
5 Videos
- SAMPLE PAPER 3BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - Section - C
5 Videos
- SAMPLE PAPER 5BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - Section -C
2 Videos
Similar Questions
If the area of the triangle is 4sq units, then x is
View SolutionIn the given figure, ABCD is a rectangle with AD=4 units and AE=EB.EF is perpendicular to DB and is half of DF . If the area of the triangle DEF is 5 sq. units, then what is the area of ABCD ? 18√3 sq. units (b) 20 sq. units (c) 24 sq. units (d) 28 sq. units
View Solution
Knowledge Check
If the area of the triangle with vertices (x, 0), (1,1) and (0,2) is 4 sq units, then the value of x is
A-2B-4C-6D8
A tangent to the curve xy=100 at a point on it forms a triangle with the coordinate axes, then the area of the triangle thus formed is
1) 100 sq.units
2) 200 sq.units
3) depending on coordinates of point of contact
4) 50 sq.units
View Solution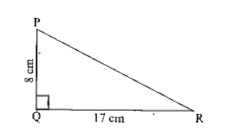
What is the area of the triangle PQR shown in the given figure?
View SolutionIf the area of the given triangle given below is 20 sq units,what are the co-ordinates of point C?
View SolutionIf the centroid and two vertices of a triangle are (4.−8),(−9,7),(1,4) respectively. Then the area of the triangle ( in sq.units) is
View SolutionThree straight lines are drawn through a point P lying inside a triangle ABC, parallel to its sides. The area of the resulting triangles are 1,4 and 9 sq units. Find the area of ΔABC in square units.
View SolutionIf the centroid and two vertices of a triangle are (4,−8),(−9,7),(1,4) and the area of the triangle (in sq.units) is "K" ,then 8333K is equal to
View SolutionIf the centroid and two vertices of a triangle are (4,-8),(-9,7),(1,4) then the area of the triangle (in sq.units ) is abc then a83=
View Solution
