For a circle having radius r, what is the area of quadrant?
πr2
(πr2+2r)
14πr2
12πr2
The correct Answer is:C
To find the area of a quadrant of a circle with radius r, we can follow these steps:
1. Understand the Circle and Quadrant:
A circle can be divided into four equal parts, known as quadrants. Each quadrant represents one-fourth of the entire circle.
2. Formula for Area of a Circle:
The area A of a circle is given by the formula:
A=πr2
where r is the radius of the circle.
3. Calculate the Area of the Quadrant:
Since a quadrant is one-fourth of the circle, we can find the area of the quadrant by dividing the area of the circle by 4:
Area of Quadrant=14×A=14×πr2
4. Simplify the Expression:
This can be simplified to:
Area of Quadrant=πr24
Final Answer:
The area of the quadrant of a circle with radius r is:
πr24
A circle can be divided into four equal parts, known as quadrants. Each quadrant represents one-fourth of the entire circle.
The area A of a circle is given by the formula:
A=πr2
where r is the radius of the circle.
Since a quadrant is one-fourth of the circle, we can find the area of the quadrant by dividing the area of the circle by 4:
Area of Quadrant=14×A=14×πr2
This can be simplified to:
Area of Quadrant=πr24
The area of the quadrant of a circle with radius r is:
πr24
Topper's Solved these Questions
- SAMPLE PAPER 3Book:OSWAL PUBLICATIONChapter:SAMPLE PAPER 3Exercise:Section -A
Explore 6 Videos
- SAMPLE PAPER 3Book:OSWAL PUBLICATIONChapter:SAMPLE PAPER 3Exercise:Section B
Explore 2 Videos
- SAMPLE PAPER 2Book:OSWAL PUBLICATIONChapter:SAMPLE PAPER 2Exercise:QUESTION BANK
Explore 99 Videos
- SAMPLE PAPER 4Book:OSWAL PUBLICATIONChapter:SAMPLE PAPER 4Exercise:Section -C
Explore 8 Videos
Similar Questions
Knowledge Check
A right angled isosceles triangle is inscribed in a circle of radius r. What is the area of the remaining portion of the circle ?
Aπr22B(π−12)r2C(π−1)r2D(π−2)r2In the adjoining figure a quadrant ( of circle ) inscribes a square of maximum possible area . If the radius of the circle be 'r' then what is the area of the square ?
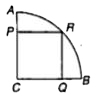 Ar22B3r25Cr2√3D2√6r
Ar22B3r25Cr2√3D2√6rFind the ratio of the area of a square inscribed in a semi-circle of radius r to the area of another square inscribed in the entire circle of radius r.
A2:1B3:2C2:5D3:5
The area of a circle varies with the square of its radius. The area of a circle having radius 3 cm is Ccm2. Find the area of the circle having redius 9 cm.
View SolutionA is the area of a circle with radius r units. Write the formula of area, making r as the subject.
View SolutionA is the area of a circle with radius r units. Write the formula of area, making r as the subject.
View SolutionThe circumference of a circle is 22 cm. Find the area of its quadrant.
View SolutionThe radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
View Solution