A new township is to be constructed along the curve y = x 3 - 11 x + 5 . Two attraction i.e., Amusement park and shopping mall is to be made on the this curve. At a point on the curve amusement park is to be constructed and on another point shopping mall is to be constructed at which tangent has the equation y=x-11.
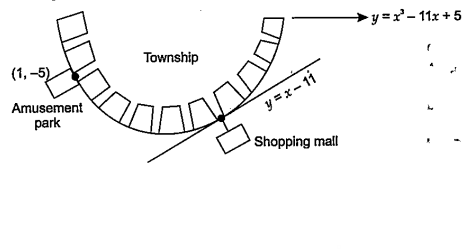
A new township is to be constructed along the curve y=x^3-11x+5. Two attraction i.e., Amusement park and shopping mall is to be made on the this curve. At a point on the curve amusement park is to be constructed and on another point shopping mall is to be constructed at which tangent has the equation y=x-11. Find the slope of the normal to the curve along which amusement park is to be constructed ?
Find the slope of the normal to the curve along which amusement park is to be constructed ?

A

1 8

B

8

C

- 8

D

- 1 8

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for A new township is to be constructed along the curve y=x^3-11x+5. Two attraction i.e., Amusement park and shopping mall is to be made on the this curve. At a point on the curve amusement park is to be constructed and on another point shopping mall is to be constructed at which tangent has the equation y=x-11. Find the slope of the normal to the curve along which amusement park is to be constructed ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSQUESTION BANK

Similar Questions

Knowledge Check

  • Point at which the tangent to the curve y=3x−2x2 has slope m=−1 is

    A(0,0)
    B(1,1)
    C(−1,1)
    D(1,−1)

  • Find the equation of the tangent y=x2+4x+1 and the normal to the curve y=x2+4x+1 at the point where x=3

    Aequation of the tangent y−10x+8=0 and equation of the normal 15x+10y−223=0
    Bequation of the tangent y−10x+8=0 and equation of the normal x+10y−223=0
    Cequation of the tangent y−10x−8=0 and equation of the normal x−10y−223=0
    Dequation of the tangent y−15x+8=0 and equation of the normal x+10y−223=0