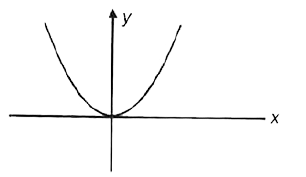
एक कण नियत चाल u से परवलयाकार पथ x2=y में गतिशील है। कण का उस क्षण त्वरण ज्ञात कीजिये जब यह मूल बिन्दु से गुजरता है तथा मूल बिन्दु पर वक्रता त्रिज्या भी ज्ञात कीजिये।
जब कण मूल बिन्दु से गुजरता है, इसका वेग x-अक्ष की ओर है, अत:
vx=u, vy=0
लेकिन चूंकि कण एकसमान चाल से गतिशील है इसलिए स्पर्श रेखीय त्वरण शून्य है।
अत: मूल बिन्दु पर ax=0,
अब y=x2
t के सापेक्ष अवकलन करने पर
dydt=2xdxdt⇒vy=2xvx
पुन: t के सापेक्ष अवकलन करने पर
dvydt=2dxdtvx+2xdvxdt
⇒ay=2v2x+0=2u2
अत: कण का त्वरण 2u2 है।
चूँकि यह त्वरण अभिकेंद्रीय त्वरण है, ∴(u2r)=2u2, जहाँ r वक्रता त्रिज्या है
⇒r=12 इकाई
Similar Questions
उस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionउन रेखाओं का समीकरण जिन पर मूल बिन्दु से डाला गया। लम्ब x-अक्ष के साथ 30∘ का कोण बनाता है और उनसे तथा x-अक्ष से बने त्रिभुज का क्षेत्रफल 50√3 वर्ग इकाई हो, है
View Solution
