1 जनवरी, 1901 को कौन-सा बार था?
सोमवार
बुधवार
रविवार
मंगलवार
The correct Answer is:D
पहली जनवरी 1 ईसा पूर्व को सोमवार था।
1 जनवरी 1901 का अर्थ है 1900 पूर्ण वर्ष एवं पहली जनवरी, 1901
1600 वर्ष में 0 विषम दिन है।
300 वर्ष में एक विषम दिन है। 1 जनवरी, 1901
⇒ सोमवार + 2 ⇒ बुधवार
Topper's Solved these Questions
- कैलेंडर और घड़ीBOOK - AGRAWAL EXAM CARTCHAPTER - कैलेंडर और घड़ीEXERCISE - परीक्षोपयोगी महत्त्वपूर्ण प्रश्न
24 Videos
- अभाषिक तर्कशक्ति BOOK - AGRAWAL EXAM CARTCHAPTER - अभाषिक तर्कशक्ति EXERCISE - परीक्षोपयोगी महत्त्वपूर्ण प्रश्न
8 Videos
- कोडिंग-डिकोडिंगBOOK - AGRAWAL EXAM CARTCHAPTER - कोडिंग-डिकोडिंगEXERCISE - परीक्षोपयोगी महत्त्वपूर्ण प्रश्न
34 Videos
Similar Questions
एक घड़ी दोपहर 1 : 30 बजे का समय दर्शा रही है। यदि मिनट की सुई दक्षिण की और हो, तो बतायें कि घण्टे की सुई किस दिशा में होगी ?
View Solutionसभी प्रश्न आकृतियों में प्रश्नवाचक चिह्र के स्थान पर संबंधित आकृति का चुनाव उत्तर आकृति से कीजिये ।
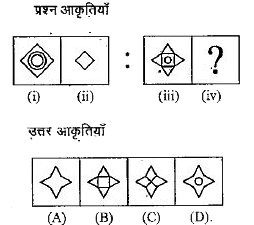
View Solutionयदि "संतरे' को 'मक्खन', 'मक्खन', को 'साबुन', 'साबुन' को 'स्याही' , 'स्याही को 'शहद' तथा 'शहद' को 'संतरा' कहा जाता है, तो निम्न में से किसका उपयोग कपड़े धोने में किया जाता है ?
View Solutionसारणिक के गुणों का प्रयोग कर ∣∣ ∣ ∣ ∣∣1a1bc1b1ca1c1ab∣∣ ∣ ∣ ∣∣ का मान निकालें |
View Solutiontan−12x1−x2=
View Solution∫−11+x2dx=
View Solutiontan−1(1)=….. ?
View Solutiontan−112+tan−114=....
View Solutioncos−1(2x−1)
View Solutionddx[tan−1√1+x2−cot−1(−√1+x2)]=
View Solutionत्रिकोणमितीय सर्वसमिकाओ को सिद्ध करो:
11+sinθ+11−sinθ=2sec2θ
View Solutionत्रिकोणमितीय सर्वसमिकाओ को सिद्ध करो :
(1+tan2θ)(1+sinθ)(1−sinθ)=1
View Solutionत्रिकोणमितीय सर्वसमिकाओ को सिद्ध करो :
(1+cot2θ)(1−cosθ)(1+cosθ)=1
View Solutionसर्वसमिकाओ को सिद्ध करो:
1cosecA−cotA−1sinA=1sinA−1cosecA+cotA
View Solutionत्रिकोणमितीय सर्वसमिकाओं को सिद्ध करो :
(1+tan2θ)(1−sinθ)(1+sinθ)=1
View Solutionत्रिकोणमितीय सर्वसमिकाओं को सिद्ध करो :
11+sinA+11−sinA=2sec2A
View Solution
