The length of a potentiometer wire is 10 m and carries steady current on connecting the sliding jockey to standard cell of 1.018 volt, the null point is obtained at the distance of 850 cm.
If the length of potentiowire is doubled, then the e.m.f. will be:
halved
doubled
not change
none of these
The correct Answer is:B
To solve the problem, we need to understand the relationship between the electromotive force (e.m.f.) of the standard cell, the length of the potentiometer wire, and the potential gradient.
1. Identify the Given Values:
- Length of the potentiometer wire (L₁) = 10 m = 1000 cm
- E.m.f. of the standard cell (E) = 1.018 V
- Null point distance (d) = 850 cm
2. Calculate the Potential Gradient (k):
The potential gradient (k) is defined as the e.m.f. per unit length of the wire. It can be calculated using the formula:
k=EL
Here, E is the e.m.f. and L is the length of the wire.
k=1.018 V1000 cm=0.001018 V/cm
3. Doubling the Length of the Potentiometer Wire:
If the length of the potentiometer wire is doubled, the new length (L₂) will be:
L₂=2×L₁=2×1000 cm=2000 cm
4. Calculate the New E.m.f. (E₂):
Since the potential gradient remains constant (as the current is steady), the new e.m.f. can be calculated using the same formula:
E₂=k×L₂
Substitute the values:
E₂=0.001018 V/cm×2000 cm=2.036 V
5. Conclusion:
The e.m.f. will be doubled when the length of the potentiometer wire is doubled. Therefore, the answer is:
E₂=2×1.018 V=2.036 V
Final Answer:
The e.m.f. will be doubled.
---
- Length of the potentiometer wire (L₁) = 10 m = 1000 cm
- E.m.f. of the standard cell (E) = 1.018 V
- Null point distance (d) = 850 cm
The potential gradient (k) is defined as the e.m.f. per unit length of the wire. It can be calculated using the formula:
k=EL
Here, E is the e.m.f. and L is the length of the wire.
k=1.018 V1000 cm=0.001018 V/cm
If the length of the potentiometer wire is doubled, the new length (L₂) will be:
L₂=2×L₁=2×1000 cm=2000 cm
Since the potential gradient remains constant (as the current is steady), the new e.m.f. can be calculated using the same formula:
E₂=k×L₂
Substitute the values:
E₂=0.001018 V/cm×2000 cm=2.036 V
The e.m.f. will be doubled when the length of the potentiometer wire is doubled. Therefore, the answer is:
E₂=2×1.018 V=2.036 V
The e.m.f. will be doubled.
Similar Questions
The potentiometer wire is of length 1200 cam and it carries a current of 60 mA. For a cell of emf 5V and internal resistance of 20Ω, the null point of it is found to be at 1000 cm.The resistance of potentiometer wire is
View SolutionThe length of a potentiometer wire is 600 cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be at 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The resistance of the voltmeter is
View SolutionThe length of a potentiometer wire is 600 cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be at 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The resistance of the voltmeter is
View SolutionThe length of a potentiometer wire is 600cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be ast 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The voltmeter reading will be
View SolutionThe length of a potentiometer wire AB is 600cm, and it carries a constant current of 40mA from A to B. For a cell of emf 2V and internal resistance 10Ω, the null point is found at 500cm from A. When a voltmeter is connected across the cell, the balancing length of the wire is decreased by 10cm.
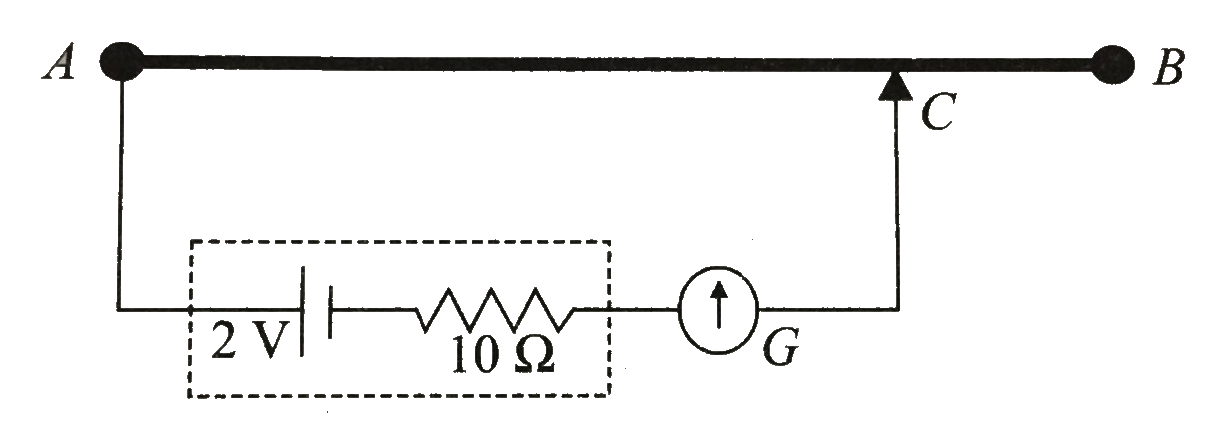
Potential gradient along AB is
View SolutionA 10 m long potentiometer wire carries a steady current. A standard cell of emf 1.018 V is balanced against a length of 254.5 cm of the wire. What is the potential gradient across the potentiometer wire ?
View SolutionThe length of potentiometer wire is 200 cm and the emf of standard cell is primary circuit is E volts. It is employed to a battery of emf 0.4 v the balance point is obtained at l = 40 cm from positive end, the E of the battery is (cell in primary is ideal and series resistance is zone
View SolutionThe length of potentiometer wire is 1m and its resistance is 4Ω. Acurrent of 5mA is flowing in it. An unknown emf is balanced on 40 cm length of this wire. The unknown emf is x mv. What is the value of .x. ?
View SolutionThe length of the potentiometer wire is 600 cm and a current of 40 mA is flowing in it. When a cell of emf 2 V and internal resistance 10Ω is balanced on this potentiometer the balance length is found to be 500 cm. The resistance of potentiometer wire will be
View SolutionPotentiometer wire PQ of 1m length is connected to a standard cell E1. Another cell E2 of emf 1.02V is connected with a resistance r and a switch S as shown in the circuit diagram. With switch S open, the null position is obtained at a distance of 51cm from P.
(i) Calculate the potential gradient of the potentiometer wire.
(ii) Find the emf of cell E1.
(iii) When switch S is closed, will the null point move toward P or toward Q? Give reason for your answer.
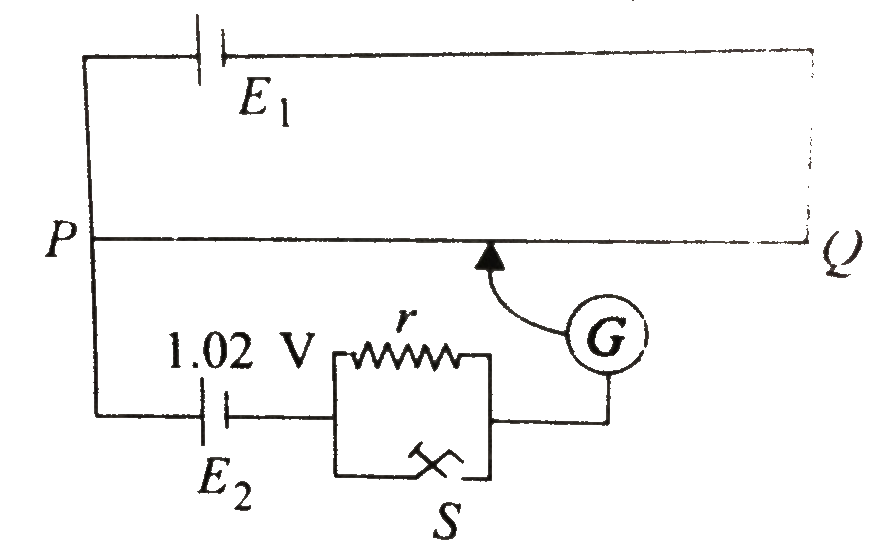
View Solution
