The drift velocity of a current carrying conductor is Vd if current flowing through the wire is halved then the value of drift velocity is:
remains same
four times
doubled
halved
The correct Answer is:D
To solve the problem, we need to understand the relationship between current (I) and drift velocity (V_d) in a current-carrying conductor. The relationship is given by the formula:
I=n⋅A⋅e⋅Vd
Where:
- I is the current,
- n is the number of charge carriers per unit volume,
- A is the cross-sectional area of the conductor,
- e is the charge of an electron,
- Vd is the drift velocity.
1. Understand the relationship: From the formula I=n⋅A⋅e⋅Vd, we can see that the current I is directly proportional to the drift velocity Vd when n, A, and e are constant.
2. Halve the current: According to the problem, the current flowing through the wire is halved. This means:
I′=I2
where I′ is the new current.
3. Relate the new current to drift velocity: Since I is directly proportional to Vd, we can express the new drift velocity V′d in terms of the original drift velocity Vd:
I′=n⋅A⋅e⋅V′d
4. Substituting the new current: Now substituting I′ into the equation:
I2=n⋅A⋅e⋅V′d
5. Expressing V′d: Since I=n⋅A⋅e⋅Vd, we can replace I in the equation:
n⋅A⋅e⋅Vd2=n⋅A⋅e⋅V′d
6. Canceling common terms: We can cancel n, A, and e from both sides (assuming they are not zero):
Vd2=V′d
7. Conclusion: Thus, the new drift velocity V′d is:
V′d=Vd2
Final Answer:
The drift velocity is halved. Therefore, the correct option is that the drift velocity becomes Vd2.
- I is the current,
- n is the number of charge carriers per unit volume,
- A is the cross-sectional area of the conductor,
- e is the charge of an electron,
- Vd is the drift velocity.
I′=I2
where I′ is the new current.
I′=n⋅A⋅e⋅V′d
I2=n⋅A⋅e⋅V′d
n⋅A⋅e⋅Vd2=n⋅A⋅e⋅V′d
Vd2=V′d
V′d=Vd2
The drift velocity is halved. Therefore, the correct option is that the drift velocity becomes Vd2.
Similar Questions
The drift velocity does not depend upon
View SolutionDefine the term 'drift velocity' of electrons in a current carrying conductor. Obtain the relationship between the current density and the drift velocity of electrons.
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionThe drift velocity of free electrons in a conductor is v, when a current i is flowing in it, Ifboth the radius and current are doubled, then the drift velocity will be :
View SolutionThe drift velocity of free elecrons in a conductor is v, when a current i is flowing in it. If both the radius and current are doubled, then the drift velocity wil be
View SolutionTwo cylindrical rods of uniform cross-section area A and 2A, having free electrons per unit volume 2n and n respectively are joined in series. A current I flows through them in steady state. Then the ratio of drift velocity of free electron in left rod to drift velocity of electron in the
right rod is (vLvR) is
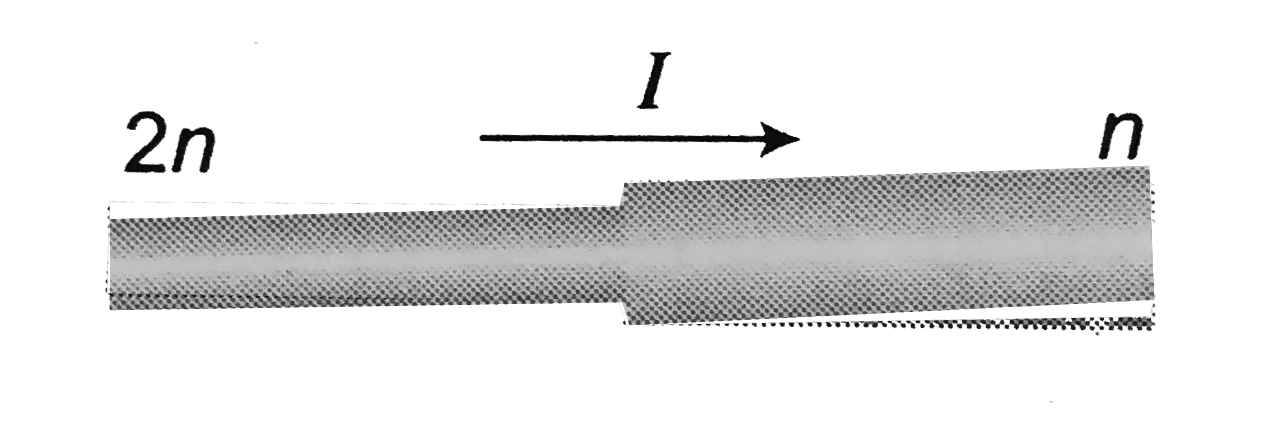
View SolutionWhen current flows through a conductor, then the order of drift velocity of electrons will be
View SolutionWhen the current i is flowing through a conductor, the drift velocity is v . If 2i current is flowed through the same metal but having double the area of cross-section, then the drift velocity will be
View SolutionWhen the current i is flowing through a conductor, the drift velocity is v . If 2i current is flowed through the same metal but having double the area of cross-section, then the drift velocity will be
View SolutionExplain the term 'drift velocity' of electrons in a conductor. Hence obtain the expression for the current through a conductor in terms of 'drift velocity'.
View Solution
