Two point charges (+2q) and (-2q) are kept inside a large metallic cube without touching its sides. Electric flux emerging out of the cube is:
4qε0
2qε0
0
qε0
The correct Answer is:C
To solve the problem of finding the electric flux emerging out of a large metallic cube containing two point charges (+2q) and (-2q), we can follow these steps:
1. Identify the Charges Inside the Cube:
- We have two point charges: one is +2q and the other is -2q.
2. Apply Gauss's Law:
- Gauss's Law states that the electric flux (Φ) through a closed surface is proportional to the net charge (Q_enc) enclosed within that surface. The formula is given by:
Φ=Qencϵ0
- Here, ϵ0 is the permittivity of free space.
3. Calculate the Net Charge Inside the Cube:
- The net charge inside the cube is calculated by summing the individual charges:
Qenc=(+2q)+(−2q)=0
4. Substitute the Net Charge into Gauss's Law:
- Since the net charge Qenc is zero, we substitute this into Gauss's Law:
Φ=0ϵ0=0
5. Conclusion:
- The electric flux emerging out of the cube is zero.
Final Answer:
The electric flux emerging out of the cube is 0.
- We have two point charges: one is +2q and the other is -2q.
- Gauss's Law states that the electric flux (Φ) through a closed surface is proportional to the net charge (Q_enc) enclosed within that surface. The formula is given by:
Φ=Qencϵ0
- Here, ϵ0 is the permittivity of free space.
- The net charge inside the cube is calculated by summing the individual charges:
Qenc=(+2q)+(−2q)=0
- Since the net charge Qenc is zero, we substitute this into Gauss's Law:
Φ=0ϵ0=0
- The electric flux emerging out of the cube is zero.
The electric flux emerging out of the cube is 0.
Similar Questions
Knowledge Check
A closed surface in vacuum encloses charges −qand+3q. The total electric flux emerging out of the surface is:
AzeroB2q/ε0C3q/ε0D4q/ε0
A short electric dipole (which consists of two point charges, +qand−q) is placed at the centre O and inside a large cube (ABCDEFGH) of length L, as shown in figure. The electric flux, emanating through the cube is :
View SolutionA charge qμC is placed at the centre of a cube of a side 0.1m, then the electric flux diverging from each face of the cube is
View SolutionA charge q is placed at the centre of a cube. What is the electric flux passing through the cube?
View Solution(A)Two point charges q1 and q2 are kept r distance apart in a uniform external electric field →E. Find the amount of work done in assembling this system of charges. (B) A cube of side 20 cm is kept in a region as shown in the figure. An electric field →E exists in the region such that the potential at a point is given by V=10x+5, where V is in volt and x is in m. Find the electric field →E and (ii) total electric flux through the cube.

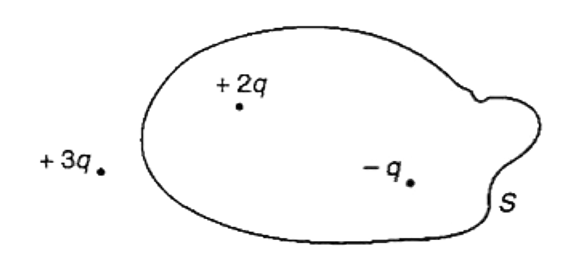
View SolutionFigure shows three point charges +2q,-q and +3q. Two charges +2q and -q are enclosed within a surface .S.. What is the electric flux due to this configuration through the surface.S?
View Solution(A): A point charge is lying at the centre of a cube of each side. The electric flux emanating from each surface of the cube is 1th6 total flux.
(R ): According to Gauss theorem, total electric flux through a closed surface enclosing a charge is equal to 1/ε0 times the magnitude of the charge enclosed.
View SolutionTwo point charges 17.7 μC and -17.7μC, separated by a very small distance, are kept inside a large hollow metallic sphere. Electric flux emanating through the sphere is:
View Solution
