A coil having 1000 turns forming square loop of side 10 cm is placed normal to magnetic field which increases at a rate of 1Ts−1 . The induced emf is:
5V
10V
2V
20V
The correct Answer is:b
To find the induced EMF in the coil, we can follow these steps:
Step 1: Identify the given values
- Number of turns (N) = 1000
- Side of the square loop (s) = 10 cm = 0.1 m (conversion to meters)
- Rate of change of magnetic field (dB/dt) = 1 T/s
Step 2: Calculate the area of one turn of the coil
The area (A) of a square loop can be calculated using the formula:
A=s2
Substituting the value of s:
A=(0.1m)2=0.01m2
Step 3: Calculate the total area of the coil
Since the coil has 1000 turns, the total area (A_total) is:
Atotal=N×A=1000×0.01m2=10m2
Step 4: Use Faraday's law of electromagnetic induction to find the induced EMF
According to Faraday's law, the induced EMF (ε) can be calculated using the formula:
ϵ=−dΦdt
Where Φ (magnetic flux) is given by:
Φ=B×A
Since the area is constant and only the magnetic field is changing, we can express the induced EMF as:
ϵ=−AdBdt
Substituting the values:
ϵ=−10m2×1T/s=−10V
(The negative sign indicates the direction of the induced EMF according to Lenz's law, but we are interested in the magnitude.)
Step 5: Conclusion
The induced EMF is:
ϵ=10V
Final Answer:
The induced EMF is 10 V.
---
- Number of turns (N) = 1000
- Side of the square loop (s) = 10 cm = 0.1 m (conversion to meters)
- Rate of change of magnetic field (dB/dt) = 1 T/s
The area (A) of a square loop can be calculated using the formula:
A=s2
Substituting the value of s:
A=(0.1m)2=0.01m2
Since the coil has 1000 turns, the total area (A_total) is:
Atotal=N×A=1000×0.01m2=10m2
According to Faraday's law, the induced EMF (ε) can be calculated using the formula:
ϵ=−dΦdt
Where Φ (magnetic flux) is given by:
Φ=B×A
Since the area is constant and only the magnetic field is changing, we can express the induced EMF as:
ϵ=−AdBdt
Substituting the values:
ϵ=−10m2×1T/s=−10V
(The negative sign indicates the direction of the induced EMF according to Lenz's law, but we are interested in the magnitude.)
The induced EMF is:
ϵ=10V
The induced EMF is 10 V.
Similar Questions
A coil having 500 square loops each of side 10 cm is placed normal to a magnetic flux which increases at the rate of 1.0 tesla/second. The induced e.m.f. in volts is
View SolutionA coil having 500 square loops each of side 10cm is placed normal to a magnetic flux which increase at the rate of 1.0teslasecond. The induced r.m.f. in volts is
View SolutionThe radius of a circular coil having 50 turns is 2 cm. Its plane is normal to the magnetic field. The magnetic field changes from 2T to 4T in 3.14 sec. The induced emf in coil will be :-
View SolutionA circular coil of wire consists of exactly 100 turns with a total resistance 0.20Ω. The area of the coil is 100cm2. The coil is kept in a uniform magnetic field B as shown in Fig. 3.212. The magnetic field is increased at a constant rate of 2Ts−1. Find the induced current in the coil in A.

View SolutionA square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
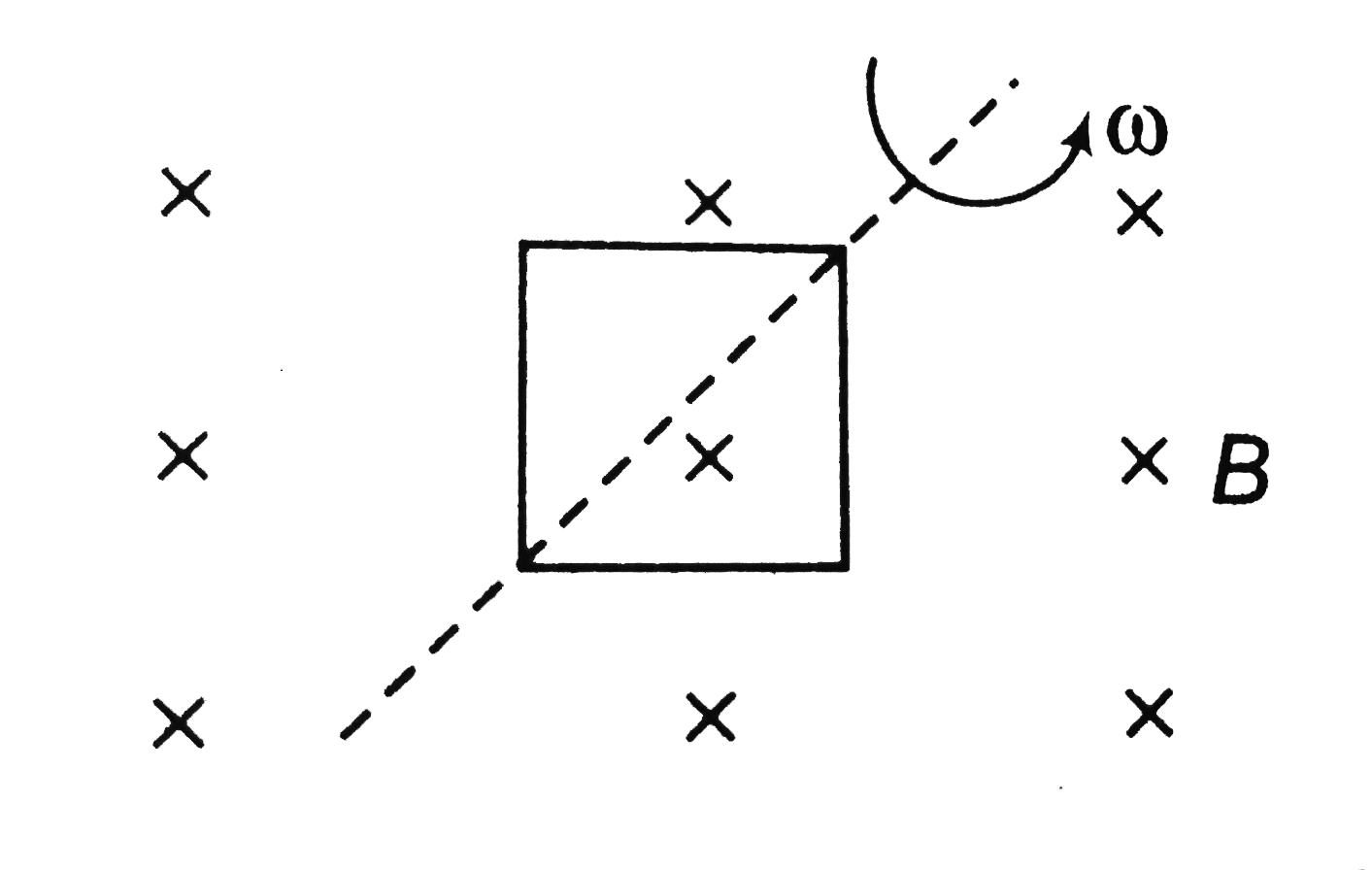
View SolutionA coil of circular cross - section having 1000 turns and 4cm2 face area is placed with its axis parallel to a magnetic field which decreases by 10−2Wb m−2 in 0.01 s. the e.m.f induced in the coil is :
View SolutionShows a coil placed in a decreasing magnetic field applied perpendicular to the plane of the coil. The magnetic field is decreasing at a rate of 10Ts−1. Find out current in magnitude and direction of current.

View SolutionShows a coil placed in a decreasing magnetic field applied perpendicular to the plane of the coil. The magnetic field is decreasing at a rate of 10Ts−1. Find out current in magnitude and direction of current.

View SolutionA semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
View SolutionA flat circular coil of 10 cm radius has 200 turns of wire. The coil is connected to a capacitor of 20μF and placed in a uniform magnetic field whose induction decreases at a constant rate of 10−2T/s. Find the capacitor's charge. The plane of the coil is perpendicular to the lines of induction of the field.
View Solution