In ΔABC, side BC = 10 cm and height AD = 4.4 cm If AC = 11 cm. then altitude BE equals -----
5 cm
4 cm
5.6 cm
5.5 cm
The correct Answer is:B
To find the altitude BE in triangle ABC, we can use the area of the triangle calculated in two different ways. Let's break down the solution step by step.
Step 1: Calculate the Area of Triangle ABC using Base BC and Height AD
The formula for the area of a triangle is given by:
Area=12×base×height
Here, we can take BC as the base and AD as the height.
Given:
- Base BC = 10 cm
- Height AD = 4.4 cm
Now, substituting the values into the area formula:
Area=12×10cm×4.4cm
Area=12×44cm2=22cm2
Step 2: Calculate the Area of Triangle ABC using Base AC and Height BE
Now, we will use AC as the base and BE as the height.
Given:
- Base AC = 11 cm
- Height BE = ?
Using the area formula again:
Area=12×base×height
22cm2=12×11cm×BE
Step 3: Solve for BE
Now, we can solve for BE:
22=12×11×BE
Multiplying both sides by 2 to eliminate the fraction:
44=11×BE
Now, divide both sides by 11:
BE=4411=4cm
Conclusion
Thus, the altitude BE equals 4 cm.
---
Area=12×base×height
- Base BC = 10 cm
- Height AD = 4.4 cm
Area=12×10cm×4.4cm
Area=12×44cm2=22cm2
- Base AC = 11 cm
- Height BE = ?
Area=12×base×height
22cm2=12×11cm×BE
22=12×11×BE
Multiplying both sides by 2 to eliminate the fraction:
44=11×BE
BE=4411=4cm
Topper's Solved these Questions
Similar Questions
In a ΔABC,AB=10cm,BC=12andAC=18 cm. Find the length of smallest altitude.
View SolutionIn a △ABC, DE is parallel to BC, AD = 3 cm, AE = 4cm and AC = 10 cm, then the value of BD in centimetres, is:
△ABC में, DE, BC & समानांतर है, AD = 3 cm, AE= 4cm और AC = 10 cm, फिर BD (सेंटीमीटर में) मान है:
View Solution
Knowledge Check
In a triangle ABC, BC = 5 cm, AC = 12 cm and AB = 13 cm. The length of the altitude drawn from B on AC is -----
A4 cmB5 cmC6 cmD7 cmIn ΔABC∠BAC=90∘ and ADI_BC. If BD=3cm and CD=4cm, then the length of AD is
A3.5 cmB5cmC2√3 cmD6cmIn Δ ABC, AB = 6 cms, BC = 10 cms, AC = 8cm and ADI_BC. Find the value of the ratio of BD:DC.
A3:4B9:16C4:5D16:25
In △ABC, AB=7 cm, BC = 10 cm, and AC = 8 cm. If AD is the angle bisector of ∠BAC , where D is a point on BC, then BD is equal to:
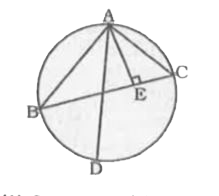
View SolutionIn the given figure , ABC is a triangle in which , AB = 10 cm , AC = 6 cm and altitude AE =4 cm . If AD is the diameter of the circumcircle , what is the length (in cm ) of circumradius ?
View SolutionIn ΔABC,AB=6cm,BC=7cm and AC=5cm .The area of ΔABC is
View SolutionIn ΔABC , if AB=16cm,BC=12cmandAC=20cm, then ΔABC is
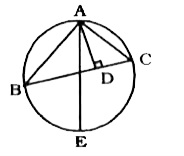
View SolutionIn the given figure, ABC is a triangle in which, AB=12cm,AC=6cmand altitude AD=4cm. If AEis the diameter of the circumcircle, than what is the length (in cm) of circum-radius?
View Solution
