The length of the shadow of a pillar is 9 m when the angle of depression of the top of the pillar is 60∘ . Find the length of the pillar
9
3√3
9√3
None of these
The correct Answer is:C
To solve the problem, we need to find the height of the pillar given the length of its shadow and the angle of depression from the top of the pillar. Here's the step-by-step solution:
Step 1: Understand the Geometry
We have a pillar (BC) and its shadow (AB). The angle of depression from the top of the pillar (point C) to the end of the shadow (point A) is 60 degrees. The length of the shadow (AB) is given as 9 meters.
Step 2: Identify the Angles
Since the angle of depression is 60 degrees, the angle of elevation from point A to point C is also 60 degrees (alternate interior angles).
Step 3: Set Up the Right Triangle
In the right triangle ABC:
- AB is the base (length of the shadow) = 9 m
- BC is the height of the pillar (which we need to find, let's denote it as H)
- Angle A (angle of elevation) = 60 degrees
Step 4: Use the Tangent Function
In triangle ABC, we can use the tangent function:
tan(Angle A)=OppositeAdjacent=BCAB
Substituting the known values:
tan(60∘)=H9
Step 5: Find the Value of Tan(60 degrees)
We know that:
tan(60∘)=√3
So, we can rewrite the equation:
√3=H9
Step 6: Solve for H
To find H, we multiply both sides by 9:
H=9⋅√3
Step 7: Final Answer
Thus, the height of the pillar is:
H=9√3 meters
Summary
The length of the pillar is 9√3 meters.
---
We have a pillar (BC) and its shadow (AB). The angle of depression from the top of the pillar (point C) to the end of the shadow (point A) is 60 degrees. The length of the shadow (AB) is given as 9 meters.
Since the angle of depression is 60 degrees, the angle of elevation from point A to point C is also 60 degrees (alternate interior angles).
In the right triangle ABC:
- AB is the base (length of the shadow) = 9 m
- BC is the height of the pillar (which we need to find, let's denote it as H)
- Angle A (angle of elevation) = 60 degrees
In triangle ABC, we can use the tangent function:
tan(Angle A)=OppositeAdjacent=BCAB
Substituting the known values:
tan(60∘)=H9
We know that:
tan(60∘)=√3
So, we can rewrite the equation:
√3=H9
To find H, we multiply both sides by 9:
H=9⋅√3
Thus, the height of the pillar is:
H=9√3 meters
The length of the pillar is 9√3 meters.
Similar Questions
Two pillars of equal heights stand on either side of a road which is 100 m wide. At a point on the road between the pillars, the angles of elevations of the tops of the pillars are 30∘and45∘. Find the height of each pillar and position of the point on the road.
View SolutionTwo pillars of equal height are on either side of a roadway which is 30 m wide. At a point on the roadway between the pillars, the elevations of the top of the pillars are 60∘ and 30∘. Find the height of the pillars and the position of the point.
View Solution
Knowledge Check
From two points , lying on the same horizontal line , the angles of elevation of the top of the pilar are θandϕ(θ<ϕ) . If the height of the pillar is h m and the two points lie on the same sides of the pillar , then the the distance between the two points is
Ah(tanθ−tanϕ) metreBh(cotϕ−cotθ) metreCh(cotθ−cotϕ) metreDh(tanθtanϕtanϕ−tanθ) metreHorizontal distance between two pillars of different heights is 60 m . It was observed that the angular elevation from the top of the shorter pillar is 45∘ . If the height of taller pillar is 130 m, the height of the shorter pillar is
A45 mB70 mC80 mD60 mFrom two points on the ground and lying on a straight line through the foot of a pillar, the two angles of elevation of the top of the pillar are complementary to each other. If the distances of the two points from the foot of the pillar are 12 metres and 27 metres and the two points lie on the same side of the pillar, then the height (in metres) of the pillar is:
A16B12C15D18
Two pillars of equal height and on either side of a road, which is 100m wide. The angles of elevation of the top of the pillars are 60o and 30o at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.
View SolutionTwo pillars of equal height are on either side of a road, which is 100 m wide. The angles of elevation of the top of the pillar are 60∘and30∘ at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.
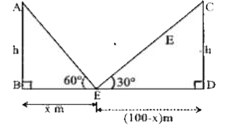
View SolutionThe length of shadow of a tree is 16m when the angle of elevation of the sun is 60∘. What is the height of the tree
View SolutionTwo pillars of equal height and on either side of a road, which is 100m wide. The angles of elevation of the top of the pillars are 60o and 30o at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.
View SolutionTwo pillars of equal height stand on either side of a roadway which is 120 m wide. At a point in the road between the pillars, the angles of elevation of the pillars are 60∘ and 30∘. Find the height of each pillars to the nearest metre and position of the point from both the pillars.
View Solution
