Electrostatic energy stored in a capacitor of 12 pF capacitance connected to a 50 V battery is:
1⋅5×10−8J
3×10−4J
1⋅5×10−10J
9×10−3J
The correct Answer is:A
To find the electrostatic energy stored in a capacitor, we can use the formula:
U=12CV2
where:
- U is the energy stored in the capacitor,
- C is the capacitance,
- V is the voltage across the capacitor.
Step 1: Identify the values of capacitance and voltage
Given:
- Capacitance C=12pF=12×10−12F
- Voltage V=50V
Step 2: Substitute the values into the formula
Now, substitute the values of C and V into the energy formula:
U=12×(12×10−12F)×(50V)2
Step 3: Calculate V2
First, calculate V2:
V2=502=2500V2
Step 4: Substitute V2 back into the formula
Now substitute V2 back into the energy formula:
U=12×(12×10−12)×2500
Step 5: Calculate the energy
Now, calculate the energy:
U=12×12×2500×10−12
Calculating 12×2500:
12×2500=30000
Now, substituting this back:
U=12×30000×10−12=15000×10−12J
Step 6: Final result
Convert 15000×10−12J to a more convenient form:
U=15×10−9J=15nJ
Thus, the electrostatic energy stored in the capacitor is:
15nJ
- U is the energy stored in the capacitor,
- C is the capacitance,
- V is the voltage across the capacitor.
Given:
- Capacitance C=12pF=12×10−12F
- Voltage V=50V
Now, substitute the values of C and V into the energy formula:
First, calculate V2:
Now substitute V2 back into the energy formula:
Now, calculate the energy:
Convert 15000×10−12J to a more convenient form:
Topper's Solved these Questions
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - B
24 Videos
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C
6 Videos
- SAMPLE PAPER 3BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - SECNTION -C
6 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C
6 Videos
Similar Questions
A 900 pF capacitor is charged by 100V battery.
(a) How much electrostatic energy is strored by the capacitor ? The capacitor is disconnected from the battery and connected to another 900 pF capacitor. How much is the electrostatic energy stored in the system ?
View SolutionA 900 pF capacitor is charged by 100V battery.
(a) How much electrostatic energy is strored by the capacitor ? The capacitor is disconnected from the battery and connected to another 900 pF capacitor. How much is the electrostatic energy stored in the system ?
View SolutionThe total electrostatic energy stored in both the capacitor is
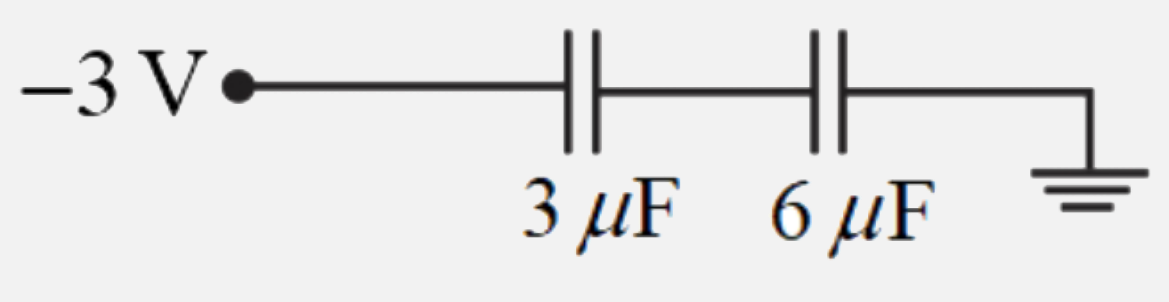
View SolutionA 12pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ? If another capacitor of 6pF is connected across the combination, find the charge stored and potential difference across each capacitor.
View SolutionA 12 pF capacitor is connected to a 50 V battery . How much electrostatic energy is stored in the capacitor ? If another capacitor of 6 pF is connected in series with it with the same battery connected across the combination , find the charge stored and potential difference across each capacitor.
View Solution(a) A parallel plate capacitor has a capacity of 6μF, with air in between the plates and 60μF when dielectric medium is introduced. What is the dielectric constant (K) of the medium?
(b) A 900 pF capacitor is charged by 100 V battery.
(i) How much electrostatic energy is stored by the capacitor?
(ii) The capacitor is now disconected from the battery and is connected to another uncharged 900 pF capacitor. How much is the electrostatic energy stored in the system?
View SolutionElectrostatic Energy Density|Capacitance|Capacitor
View SolutionTwo identical capacitors of 12 pF each are connected in series across a 50 V battery. Calculate the electrostatic energy stored in the combination. If these were connected in parallel across the same battery, find out the value of the energy stored in this combination.
View SolutionTwo identical capacitors of 10 pF each are connected in series across a 50 V battery. Calculate the electrostatic energy stored in the combination. If these were connected in parallel across the same battery, find out the value of the energy stored in this combination.
View SolutionObtain the expression for the energy stored in a capacitor connected across a dc battery. Hence define energy density of the capacitor.
View Solution
