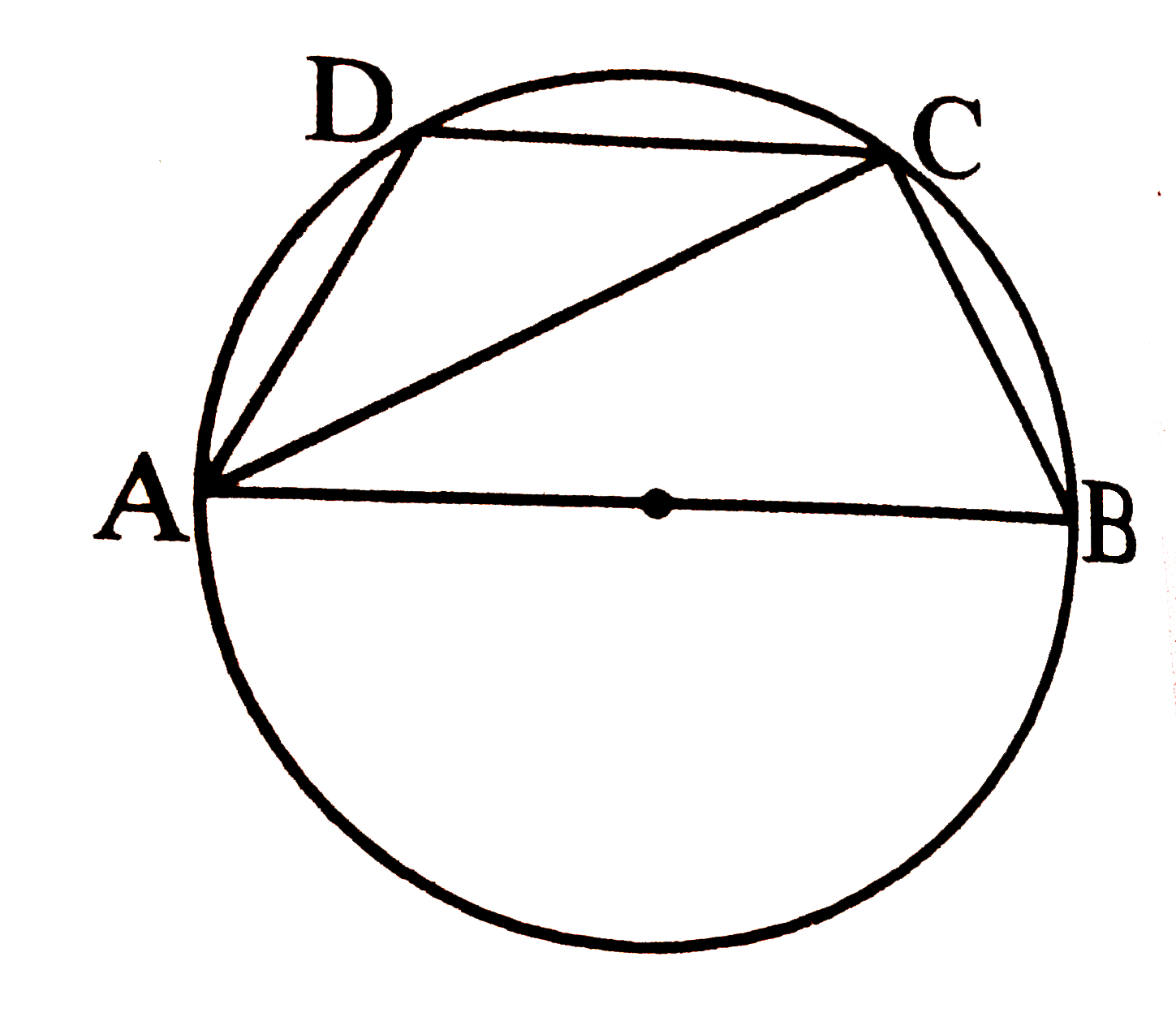AB is a diameter of a circle and ABCD is a cyclic quadrilateral in that. If ∠ACD=40∘, then measurement of ∠BAD is:
40∘
80∘
90∘
50∘
The correct Answer is:D
To solve the problem, we need to find the measurement of angle ∠BAD given that ∠ACD=40∘ and AB is the diameter of the circle.
1. Understand the properties of the circle: Since AB is the diameter, any angle inscribed in the semicircle will be a right angle. Thus, ∠ACB is 90∘.
Hint: Remember that an angle inscribed in a semicircle is always a right angle.
2. Identify the angles in the cyclic quadrilateral: In cyclic quadrilaterals, the opposite angles are supplementary. This means that ∠ACD+∠ABD=180∘.
Hint: Use the property of cyclic quadrilaterals where opposite angles sum to 180∘.
3. Calculate ∠ACB: We already established that ∠ACB=90∘.
4. Find ∠BCD: Since ∠ACD=40∘, we can find ∠BCD using the triangle ACB:
∠BCD=∠ACB−∠ACD=90∘−40∘=50∘.
Hint: Remember that the angles in a triangle sum up to 180∘.
5. Use the property of cyclic quadrilaterals: Now, we can use the cyclic quadrilateral property to find ∠BAD:
∠BAD+∠BCD=180∘.
Substituting ∠BCD=50∘:
∠BAD+50∘=180∘.
6. Solve for ∠BAD:
∠BAD=180∘−50∘=130∘.
Hint: Always isolate the variable to find its value.
7. Final Calculation: Thus, the measurement of ∠BAD is 130∘.
Conclusion:
The measurement of ∠BAD is 130∘.
∠BCD=∠ACB−∠ACD=90∘−40∘=50∘.
∠BAD+∠BCD=180∘.
Substituting ∠BCD=50∘:
∠BAD+50∘=180∘.
∠BAD=180∘−50∘=130∘.
The measurement of ∠BAD is 130∘.
Similar Questions
Knowledge Check
In the given figure PAQ is the tangent of the circle at point A and ABCD is a cyclic quadrilateral.
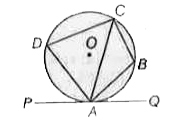
If ∠CAQ=70∘, then ∠ABC isA110∘B70∘C80∘D90∘PQ is a diameter and PQRS is a cyclic quadrilateral, if ∠PSR=150∘, then measure of ∠RPQ is
 A90∘B60∘C30∘DNone of these
A90∘B60∘C30∘DNone of theseABCD is a cyclic quadrilateral and AD is a diameter. If ∠DAC=55∘ then value of ∠ABC is
A55∘B35∘C145∘D125∘
If ABCD is a cyclic quadrilateral, then tanA+tanC=_________.
View SolutionIn a given figure, ABCD is cyclic quadrilateral, in which ∠DAB=80∘, then measures of ∠DCE is

View SolutionABCD is a cyclic quadrilateral in which AB is a diameter , ,BC=CDand∠ABD=50∘ then ∠DBC is :
View SolutionIn the given figure, ABCD is a cyclic quadrilateral and AB is diameter. ∠ADC=140∘, then find ∠BAC :

View SolutionABCD is a cyclic quadrilateral in which AB is a diameter, BC = CD and ∠A=50∘ then ∠DBC is :
View Solution