If a=√(2013)2+2013+2014, then the value of a is
1007
2013
2014
1002
The correct Answer is:C
To solve the problem a=√(2013)2+2013+2014, we will follow these steps:
Step 1: Write down the expression
We start with the expression for a:
a=√(2013)2+2013+2014
Step 2: Simplify the expression inside the square root
We can combine the constants 2013 and 2014:
2013+2014=4027
Thus, we can rewrite the expression as:
a=√(2013)2+4027
Step 3: Calculate (2013)2
Now, we calculate (2013)2:
(2013)2=4052169
So, we substitute this value back into the expression:
a=√4052169+4027
Step 4: Add the values inside the square root
Next, we add 4052169 and 4027:
4052169+4027=4056196
Now, we have:
a=√4056196
Step 5: Calculate the square root
Finally, we need to calculate the square root of 4056196:
a=2014
Conclusion
Thus, the value of a is:
2014
We start with the expression for a:
a=√(2013)2+2013+2014
We can combine the constants 2013 and 2014:
2013+2014=4027
Thus, we can rewrite the expression as:
a=√(2013)2+4027
Now, we calculate (2013)2:
(2013)2=4052169
So, we substitute this value back into the expression:
a=√4052169+4027
Next, we add 4052169 and 4027:
4052169+4027=4056196
Now, we have:
a=√4056196
Finally, we need to calculate the square root of 4056196:
a=2014
Thus, the value of a is:
2014
Similar Questions
Let αk where k=0,1,2,....,2013 are 2014th roots of unity. If z1andz2 be any two complex number such that |z1|=|z2|=1√2014 , then the value of 2013∑k=0∣∣z1+αkz2∣∣2 , is equal to
View SolutionIf x+siny=2014 and x+2014cosy=2013,0≤y≤π2 , then find the value of [x+y]−2005
(where [.] denotes greatest integer function)
View Solution
Knowledge Check
If a=√(2013)2+2013+2014 ,then value of a is
A1002B1007C2013D2014If x=2015,y=2014andz=2013, then the value of x2+y2+z2−xy−yz−zx is :
AA)3BB)4CC)6DD)2If m=(2013)! then the value of 1log2m+1log3m+........+1log2013m is equal to
A1B(2013)!C1(2013)!DNone of these
Let f(θ)=11+(tanθ)2013 then value of89∘∑θ=1∘f(θ) equals
View Solutiona, b, c are digits of a 3-digit number such that 64a + 8b + c = 403, then the value of a + b + c + 2013 is
View SolutionIf a,b are natural numbers such that 2013+a2=b2, then the minimum possible value of ab is: (A). 671 (B). 668 (C). 658 (D). 645
View SolutionIf α and β are the roots of x2−x+1=0 then the value of α2013+β2013 is equal to
View SolutionThe given Bar graph presents the Export of Tea and Coffe ( in million kg ) for the years 2012 to 2016.
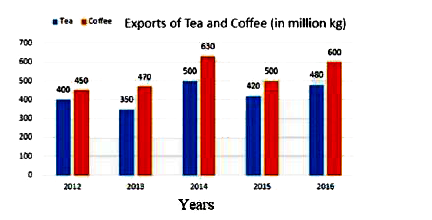
What is thr ratio of total export of tea in 2012 , 2014 and 2015 to the total export of coffee in 2013 and 2014 ?
View Solution