In the adjoining figure, if the centre of a circle are joined by horizontal and vertical lines ,then find the number of squares that can be formed .

A
6
B
7
C
8
D
1
Video Solution
Text Solution
The correct Answer is:C
The figure may be labelled as shown.
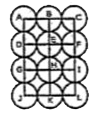
We shall join the centres of all the circles by horizontal and vertical lines and then label the resulting figure as shown.
The simplest squares are ABED, BCFE, DEHG, EFIH, GHKJ and HILK i.e. 6 in number,
The squares composed of four simple squares are ACIG and DFLJ i.c. 2 in number.
Thus, 6+2 = 8 squares will be formed,
|
Similar Questions
Knowledge Check
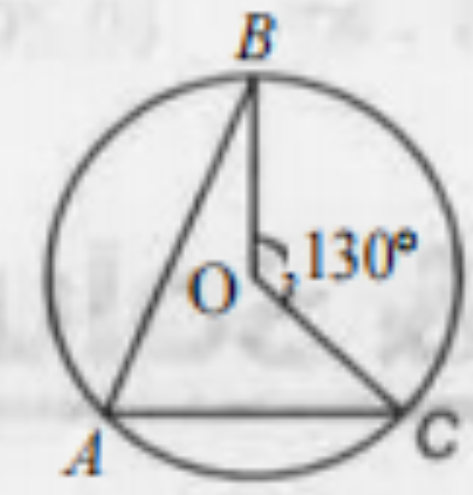
In the adjoining figure, O is the centre of the circle, Then x=?
 Az+yBz−yCy−zDnone of these
Az+yBz−yCy−zDnone of theseIn the adjoining figure, O is the centre of the circle and D ∠OBD=50∘. Find the ∠BAD :
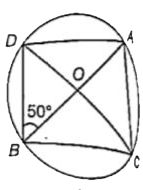 A60∘B40∘C80∘D45∘
A60∘B40∘C80∘D45∘In the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.
 A=60∘B=45∘C=30∘D=50∘
A=60∘B=45∘C=30∘D=50∘
In the adjoining figure , O is the centre of the circle. If ∠ACB=25∘, then find ∠AOB.
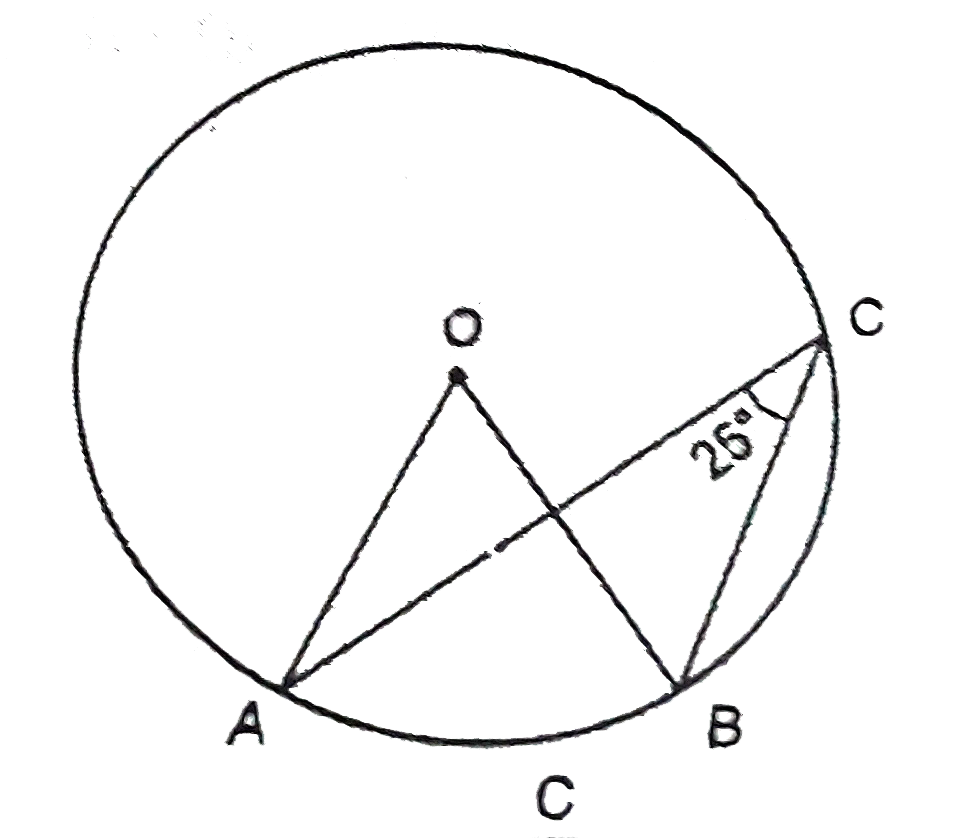
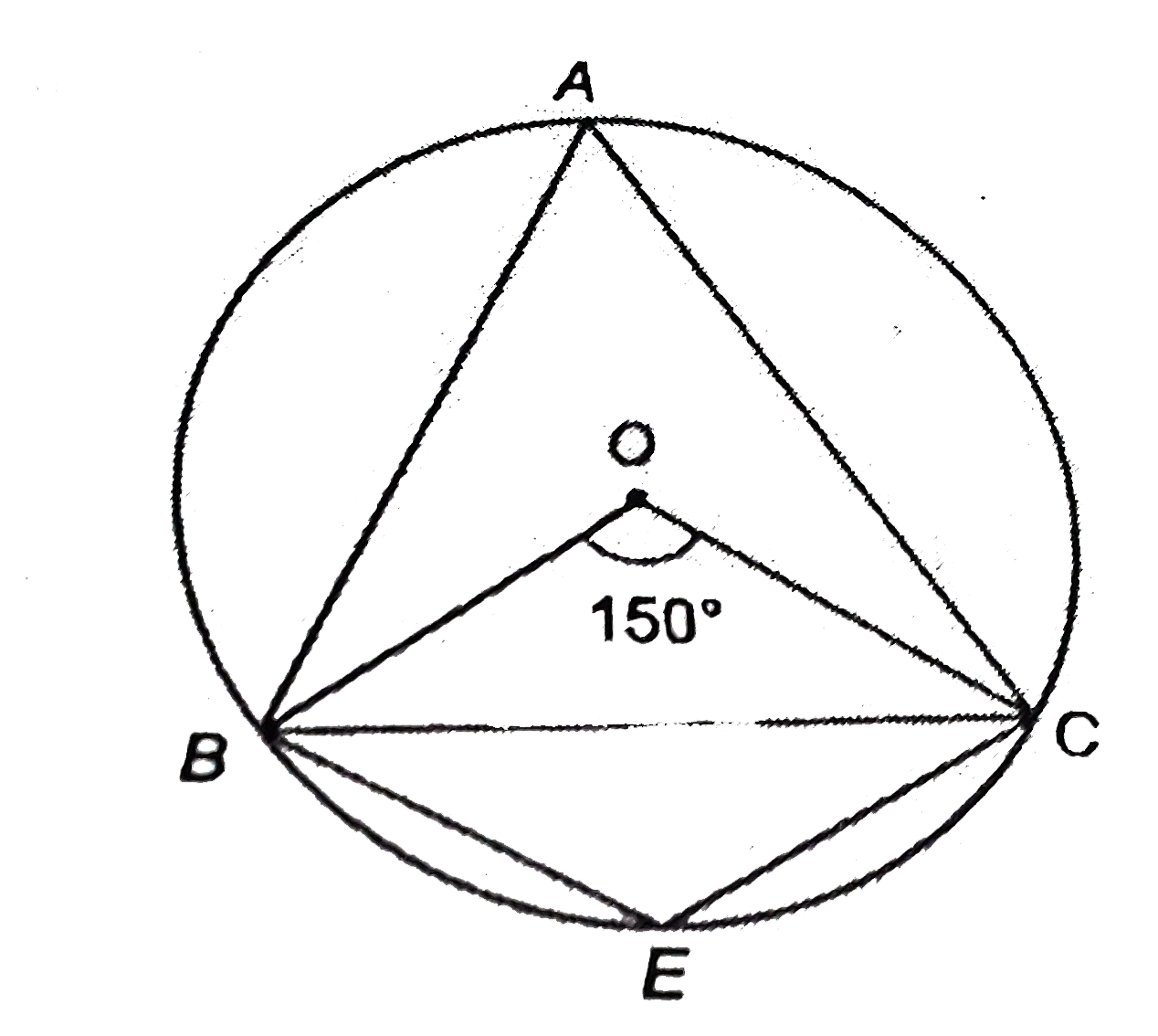
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=150∘ and ∠BOC=100∘, then find the value of ∠ABC.

View SolutionIn the adjoining figure, O is the centre of the circle. If ∠PAO=15∘ and ∠PBO=30∘, then find the value of ∠AOB.

View SolutionIn the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
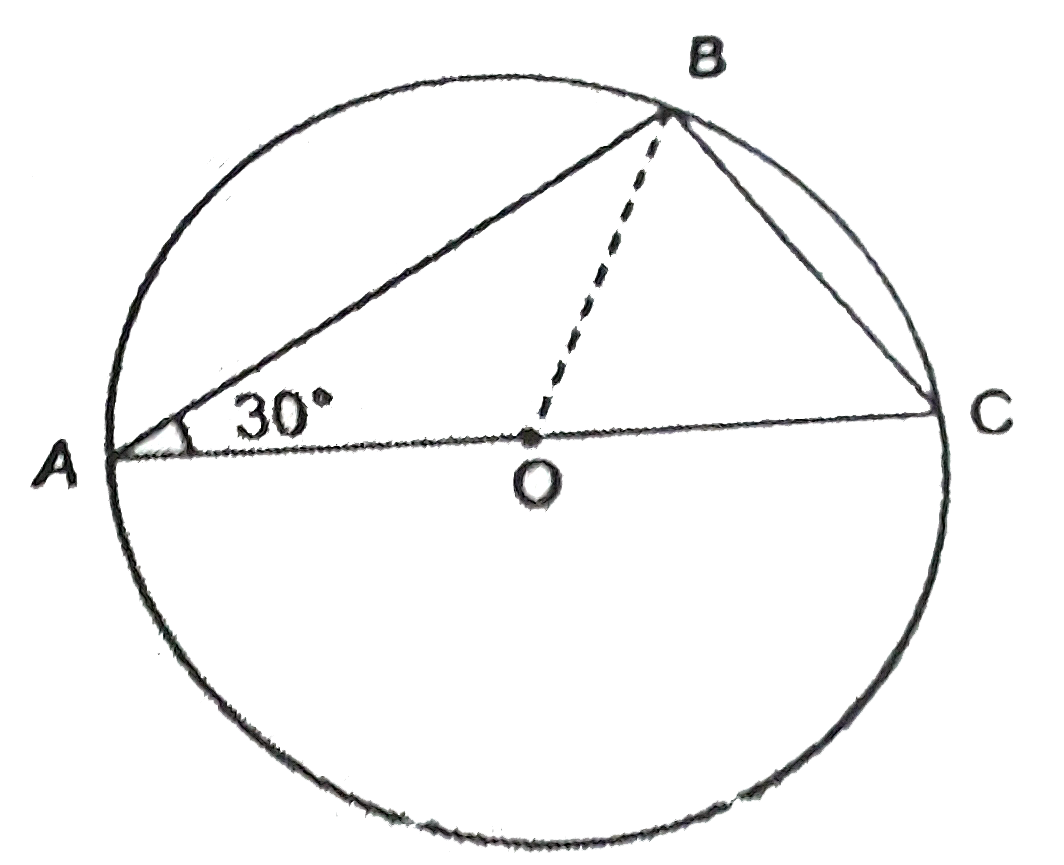
View SolutionIn the adjoining figure O is the centre of the circle . If chord AB=2 cm radius OA=2 cm, then find the value of ∠ACB.

View Solution