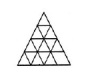
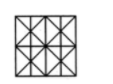
What is the minimum number of different colours required to paint he given figure such that no two adjacent regions have the same colour ?
A
3
B
4
C
5
D
6
Video Solution
Text Solution
The correct Answer is:A
The figure may be labelled as shown.

The regions A, C, E and G can have the same colour say colour .
The regions B, D, F and H can have the same colour (but different from colour 1) say colour 2. The region 1 lies adjacent to each one of the regidas A, B, C, D, E, F, G and H and therefore it should have a different colour say colour 3. A The regions J, L and N can have the same colour different from colour 3) say colour
1. The regions K, Mand O can have the same colour (different fromthe colours 1 and 3). Thus, these regions will have colour
2. The region cannot have any of the colours 1 and 2 as it lies adjacent to each one of the regions J, K, L, M, N and O and so it will have dolour
3. The region Q can have any of the colours 1 or 2.
Minimum number of coloursyequired is 3
|
Similar Questions
Knowledge Check
The minimum number of colours required to paint all the sides of a cube so that no two adjacent faces may have the same colours is :
A3B6C4D2How many minimum number of colours will be required to paint all the sides of a cube without the adjacent sides having the same colours ?
A1B2C3D4What is the minimum number of lines required to create the following figure ?
 A6B9C8D5
A6B9C8D5
What is the minimum number of lines required to make the following figure?
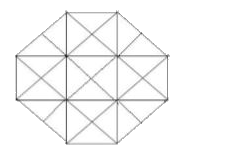
View SolutionThe minimum number of straight lines required to construct the given figure is______ .
View SolutionHow many minimum number of colours will be required to paint all the sides of a cube without the adjacent sides having the same colours ?
View SolutionWhat is the minimum number of lines required to create the following figure?
View SolutionIn how many ways can the four walls of a room be painted with three colours such that no two adjacent walls have the same colour?
View Solution