In a given question below is a statement followed by two conclusions numbered I and II. You have to assume everything in the statement to be true, then consider the two conclusions together and decide which of them logically follows beyond a reasonable doubt from the information given in the statement.
Give answer
(a) if only conclusion I follows, (b) if only conclusion II follows,
(c) if either I or II follows,
(d) if neither I nor II follows: and
(e) if both I and II follow
Statement: If all players play to their full potential, we will win the match. We have won the match.
Conclusion: I. All players played to their full potential.
II. Some players did not play to their full potential.
if only conclusion I follows
if only conclusion II follows
if either I or II follows
if neither I nor II follows
The correct Answer is:A
Conc I follows as match can be won only if all the players play to their full potential
Conc II does not follow because it contradicts the given statement
Topper's Solved these Questions
- STATEMENT AND CONCLUSIONSBOOK - LUCENT PUBLICATIONCHAPTER - STATEMENT AND CONCLUSIONSEXERCISE - EXERCISE -2
25 Videos
- STATEMENT AND CONCLUSIONSBOOK - LUCENT PUBLICATIONCHAPTER - STATEMENT AND CONCLUSIONSEXERCISE - EXERCISE -2
25 Videos
- STATEMENT AND ASSUMPTIONSBOOK - LUCENT PUBLICATIONCHAPTER - STATEMENT AND ASSUMPTIONSEXERCISE - EXERCISE-2
16 Videos
- STATEMENT AND COURSES OF ACTIONBOOK - LUCENT PUBLICATIONCHAPTER - STATEMENT AND COURSES OF ACTIONEXERCISE - EXERCISE-2
8 Videos
Similar Questions
He possesses wealth, therefore he is rich
View SolutionHe possesses wealth, therefore he is rich
View SolutionIn this question below is given a statement followed by three assumption numbered I II and III. you have to considered the statement and the following assumptions decide which of the assumptions is implicit in the statement and choose your answer accordingly.
Statement: Bill clinton is the second democrat to be re elected as president of America. The other being the legendary Roosevelt.
Assumption IN. Clinton has the same qualities that Roosevelt had.
II. The majority of people in America have faith in Clinton.
III. The election campaign of clinton's rivals was not impressive.
(a) Only I is implicit.
(b) Only II is implicit.
[c] Only III is implicit.
(d) either I or III is implicit.
(e) Either II or III is implicit..
View SolutionIn given statement followed by three courses of action numbered I,II and III. You have to assume everything in the statement to be true, then decide which of the three suggested courses of action logically follows for pursuing.
Statement Drinking water supply to New Bombay has been suspended till further orders from Maharashtra Pollution Control Board following pollution of Patalganga river,caused by discharge of effluents from some chemical industries.
Courses of action I. The industries responsible for discharging effluents into the river should be asked to close down immediately.
II. The river water should immediately be treated chemically before resuming supply.
III. The Pollution Control Board should check the nature of effluents being discharged into the river by industries at regular intervals.
(a) Only I follows
(b) Only II and III follow
(c) Only III follows
(d) All follow
(e) None of these
View Solutionदिए गए चित्र में दिखाए गए परिपथ में लगी बैटरी का विधुत वाहक बल्ब 12 बोल्ड तथा आन्तरिक प्रतिरोध नगण्य है । अमीटर Aके पाठ्यांक की गणना कीजिए जबली कुँजी K (i) खुली हो , (ii) बन्द हो ।
View Solutionदिए गए परिपथ में धारा I का मान ज्ञात कीजिये ?
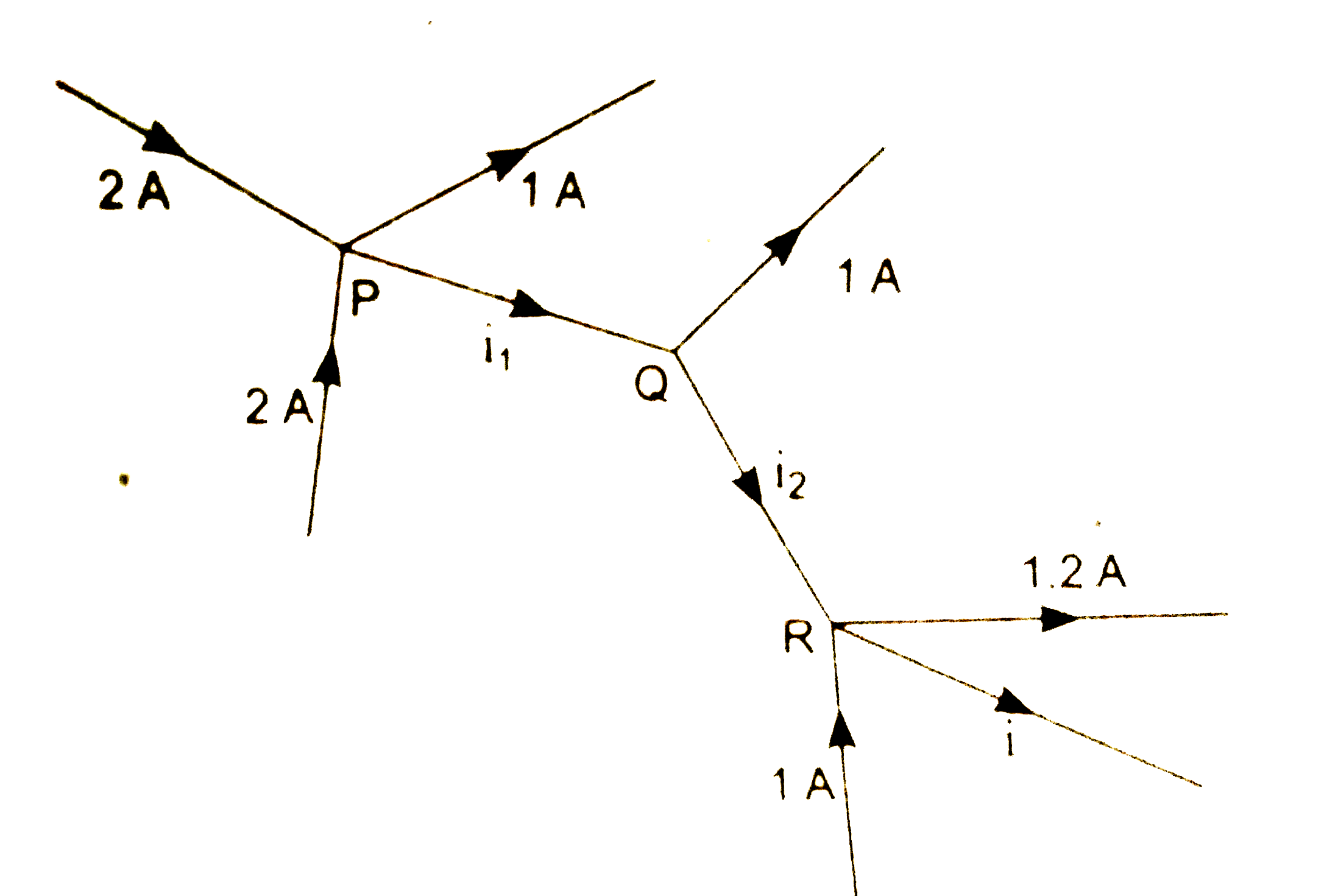
View Solutionदिए गये विघुत परिपथ की सहायता से ज्ञात कीजिए
- (i) परिपथ में धारा , तथा
(ii) बिन्दु A तथा B के बीच विभवान्तर ।
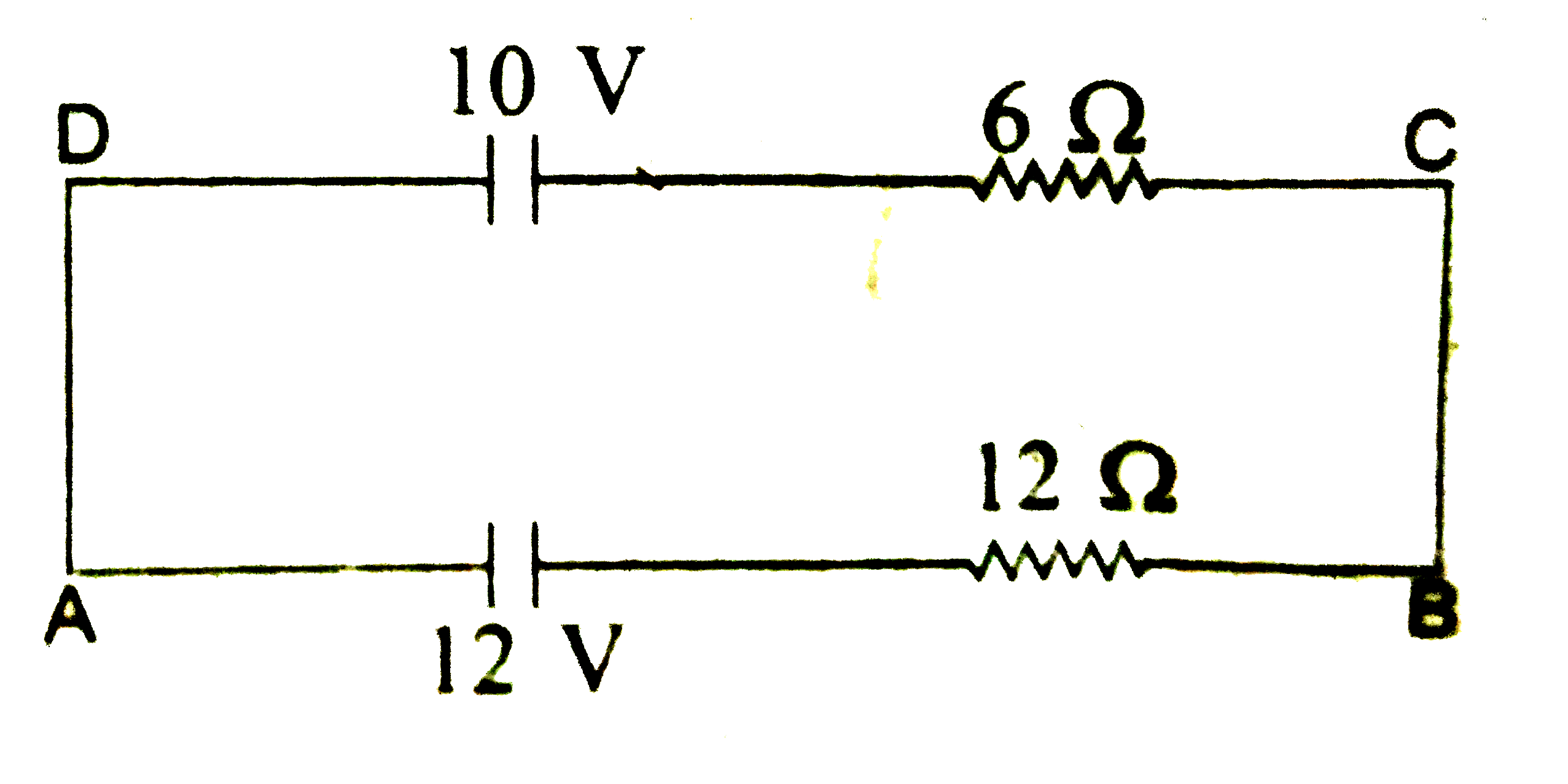
View Solutionएक स्थिर इलेक्ट्रॉन पर क्या प्रभाव होगा यदि (i ) एक चुम्बकीय क्षेत्र लगाया जाता है, (ii ) एक वैधुत क्षेत्र लगाया जाता है?
View Solutionलेन्ज का नियम द्रव्यमान, संवेग, ऊर्जा में से किसके संरक्षण नियम का पालन करता है ?
View Solutionएक प्रेरक के बहने वाली धारा, i=4+12t द्वारा दी जाती है, जहाँ I ऐम्पियर में तथा t सेकण्ड में है | इसमें स्वप्रेरित विधुत वाहक बल 12 mV है | ज्ञात कीजिए- (i) स्वप्रेरकत्व, तथा (ii) t=1 सेकण्ड पर प्रेरक में संचित ऊर्जा एवं इसको प्रदान की गयी शक्ति |
View Solutionप्रत्यावर्ती परिपथ के शक्ति गुणांक क्या होगा , यदि परिपथ में , (i ) शुद्ध प्रतिरोधी हो (ii ) शुद्ध प्रेरकीय हो ?
View Solutionएक व्यक्ति ₹ 1000 का नोट लेकर बैंक जाता है। वह कैशियर से बदले में केवल ₹5 और ₹10 के नोट देने के लिये कहता है। यदि उसे कुल ।75 नोट मिलते हैं, तो उसने ₹5 और ₹10 के कितने-कितने नोट प्राप्त किए?
View Solutionएक रेखिक समीकरण दी गई है । दो चरो में एक ऐसी और रेखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि:
(i)प्रतिच्छेद करती रेखाए हो।
(ii) समान्तर रेखाए हो।
(iii) सम्पती रेखाए हो|
View Solutionनिम्नलिखित समीकरणों के अनुसार धातु A,B,C,D व H2 की विधुत - रासायनिक श्रेणी का निर्माण करो ।
(i) 2A+2HCl→2ACl+H2
(ii) B+2HCl→BCl2+H2
(iii) 2A+BCl2→2ACl+B
(iv) D+CCl2→DCl2+C
(v) D+HCl→ कोई अभिक्रिया नहीं
View Solutionएक अभिक्रिया इस प्रकार से है -
2Ag++Cd→2Ag+Cd2+
अभिक्रिया Ag+/Ag व Cd2+/Cd के लिए मानक अपचयन विभव +0.80 तथा −0.40V है | (a) सेल का मानक वाहक बल (E∘)क्या है ?
(b) यदि Cd की सांद्रता 1M से घटाकर 0.1 M कर दें तो विधुत वाहक बल पर क्या प्रभाव होगा ?
View Solutionतीन तत्वों के E∘O.P. इस प्रकार है -
I=2.92V, II=0.76V, III=−2.65V
इनमे से कौन - सा प्रबलतम ऑक्सीकारक होगा व कौन प्रबलतम अपचायक ?
View Solution
