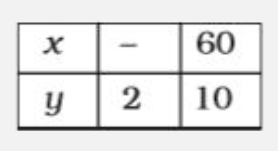
If x varies as y then x2+y2 varies as
x + y
x - y
x2−y2
None of these
To solve the problem, we need to determine how x2+y2 varies when x varies as y.
1. Understanding the Variation:
Since x varies as y, we can express this relationship mathematically as:
x=k⋅y
where k is a constant of proportionality.
2. Substituting the Relationship:
We will substitute x in the expression x2+y2:
x2+y2=(k⋅y)2+y2
3. Expanding the Expression:
Now, we expand the expression:
x2+y2=k2⋅y2+y2
4. Factoring the Expression:
We can factor out y2 from the expression:
x2+y2=(k2+1)⋅y2
5. Identifying the Variation:
Since (k2+1) is a constant, we can conclude that:
x2+y2 varies as y2
Conclusion:
Thus, we find that x2+y2 varies as y2.
Since x varies as y, we can express this relationship mathematically as:
x=k⋅y
where k is a constant of proportionality.
We will substitute x in the expression x2+y2:
x2+y2=(k⋅y)2+y2
Now, we expand the expression:
x2+y2=k2⋅y2+y2
We can factor out y2 from the expression:
x2+y2=(k2+1)⋅y2
Since (k2+1) is a constant, we can conclude that:
x2+y2 varies as y2
Thus, we find that x2+y2 varies as y2.
Similar Questions
Knowledge Check
If x varies as mth power of y, y varies as nth power of z and x varies as pth power of z then which one of the following is true?
Ap=m+nBp=m−nCp=mnDNone of theseIf x varies inversely a (y2−1) and is equal to 24 when y = 10 then the value of x when y = 5 is
A99B12C24D100Position of a particle varies as y=cos2ωt−sin2ωt. It is
Aharmonic but not SHMBSHM with period (πω)CSHM with period (2πω)Dperiodic with period (πω) but not SHM.
If x varies as y, then which of the following is/are correct?
1. x2+y2 varies as x2−y2
2. xy2 varies inversely as y
3. n√x2y varies as 2n√x4y2
Select the correct answer using the code given below :
View SolutionIf a quantity y varies as the sum of three quantities of which the first varies as x, the second varies as −x+x2 the third varies as x3−x2 then what is y equal to ?
View Solution[ 24.The length of sub-normal to the curve xy=a^(2) at (x,y) on it varies as [ 1) x^(2), 2) y^(2), 3) x^(3), 4) y^(3)]]
View SolutionIf x varies inversely as y and when x = 6, y = 8, then for x = 8 the value of y is 10.
View SolutionPosition of a particle varies as y=cos2ωt−sin2ωt. It is
View Solution