Four rods of equal length l and mass m each forms a square as shown in figure
Moment of inertia about three axes 1,2 and 3 are say I1,I2andI3. Then, match the following columns

Column-IColumn-II(A)I1(p)43ml2(B)I2(q)23ml2(C)I3(r)12ml2(s)None
A-Q,B-S,C-Q
A-S,B-Q,C-Q
A-Q,B-Q,C-S
A-R,B-Q,C-S
The correct Answer is:A
I1=2(ml212)+2(m)(I2)2=23ml2
I2=0+2(ml23)+ml2=(53)ml2
I3=4[ml23sin245∘]=23ml2=I1
Note: I1=I3(think why?)
Topper's Solved these Questions
Similar Questions
Four rods of equal length l and mass m each form a square as shown in figure. Moment of inertia about three axes 1,2 and 3 are say I1,I2 and I3 . Then, match the following
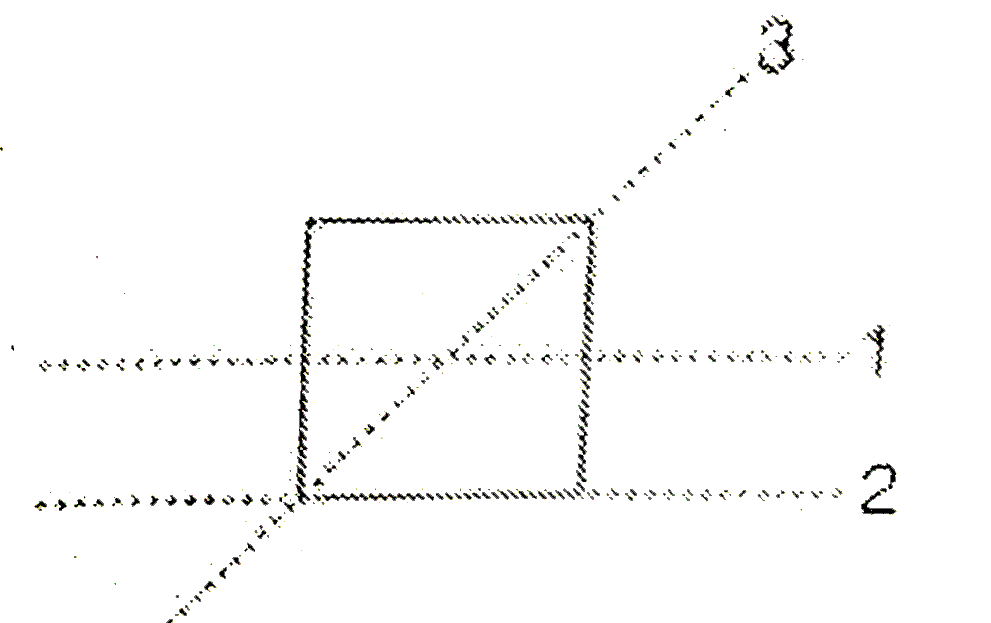

View SolutionA semicircular ring has mass m and radius R as shown in figure. Let I1,I2,I3andI4 be the moments of inertia of the four axes as shown. Axis 1 passes through centre and is perpendicular to plane of ring. Then, match the following columns.

Column-IColumn-II(A)I1(p)mR22(B)I2(q)(3/2)mR2(C)I3(r)mR2(D)I4(s)Data is insufficient
View Solution
Knowledge Check
A square lamina is as shown in figure. The moment of inertia of the frame about the three axes as shown in figure I1,I2andI3 respectively. Select the correct alternative.
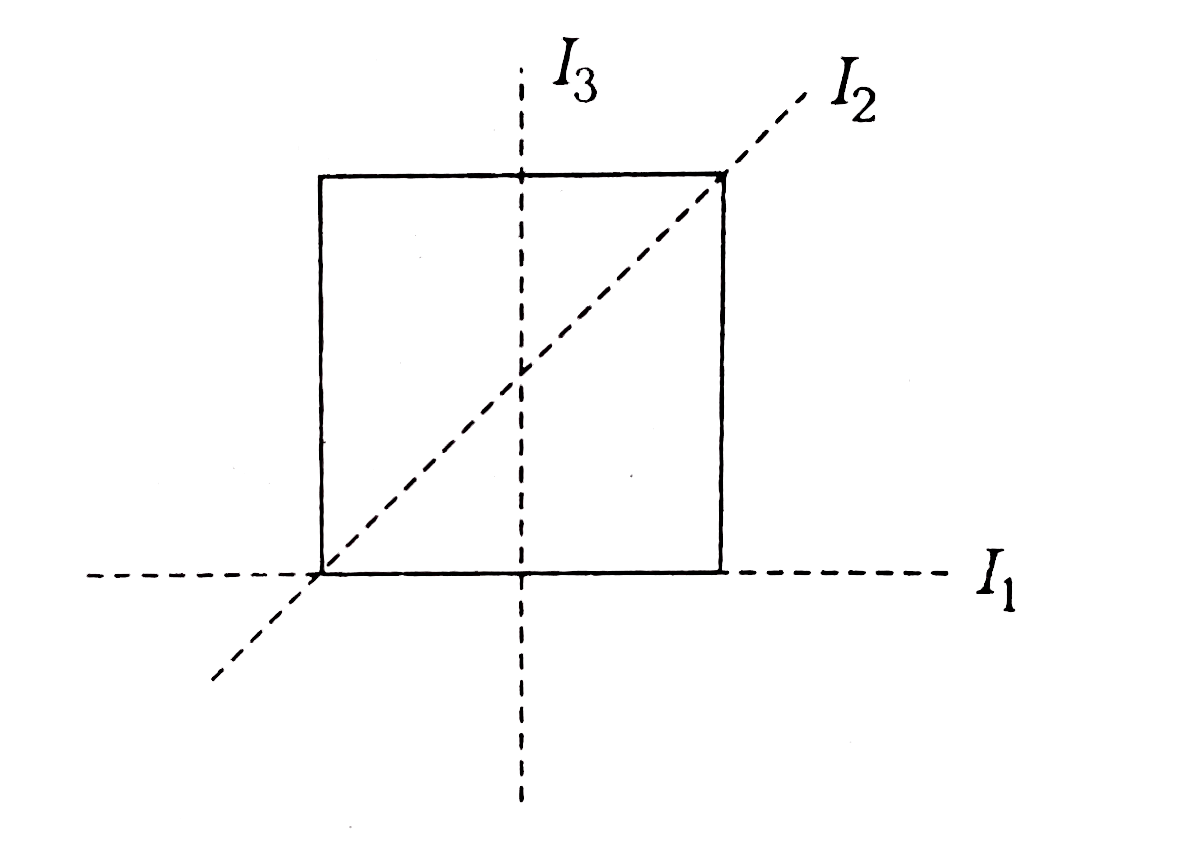 AI2=I2>I1BI1>I2>I3CI2=I3<I1DI1<I2<I3
AI2=I2>I1BI1>I2>I3CI2=I3<I1DI1<I2<I3Match the following:
Column-IColumn-II(P) R.M.S(1)23NKT(Q) PV(2)KT(R) Average K.E.(3)√3PVM(S) Most probable speed(4)√2RTMAPQRS1243BPQRS2143CPQRS3124DPQRS4123
Match the following :
Column-IColumn-II(A)3s1(p)n=3(B)3p1(q)l=0(C)4s1(r)l=1(D)4d1(s)m=0(t)m=±1
View SolutionMatch the following columns.
Column IColumn IIA.Teslap[ML2A−2T−2]B.Weberq[MLA−2T−1]C.Weber m−2q.[MA−1T−2]D.Henrys.None
View SolutionMatch the column I and II (Matrix)
Column IColumn II(a)−NO2(p)m effect(b)−O−(q)+m effect(c)−O−CH3(r)−I effect(d)−C≡N(s)−Ieffect
View SolutionMatch the species in Column I with the type of hybrid orbitals in Column II.
Column IColumn II(i)BF3(a)sp3d(ii)H2O(b)sp2(iii)PCl5(c)sp3d2(iv)SF6(d)sp3
View SolutionColumn IColumn II(A)Work(p)[A1/2T−1](B)Moment of inertia(q)[FA1/2](C)Velocity(r)[FA1/2T2]
View SolutionIf a2=5,b3=5, then
Column - IColumn - II(A) ab(p) 50(B) ab(q) 32(C) a2+b2(r) 6(D) 1(1a+1b)(s) 23(t) 325(u) 150
View Solution

