The surface charge densities on two square plates of a parallel plate capacitor are to +σand−σ respectively. What is the magnitude of the electric field in the region between the plates?
σ2ε0
σε0
0
None of these
The correct Answer is:B
To find the magnitude of the electric field in the region between two plates of a parallel plate capacitor with surface charge densities of +σ and −σ, we can follow these steps:
Step 1: Understand the Electric Field Due to a Single Plate
The electric field E due to a single infinite plane sheet of charge with surface charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
Step 2: Determine the Electric Fields from Each Plate
For the positive plate with charge density +σ:
- The electric field E1 due to this plate is directed away from the plate (upward if we consider the positive plate on the bottom):
E1=σ2ϵ0
For the negative plate with charge density −σ:
- The electric field E2 due to this plate is directed towards the plate (downward if we consider the negative plate on the top):
E2=σ2ϵ0
Step 3: Combine the Electric Fields in the Region Between the Plates
In the region between the plates, the electric fields due to both plates add up because they are in the same direction (from the positive plate to the negative plate):
Etotal=E1+E2=σ2ϵ0+σ2ϵ0=σϵ0
Step 4: Conclusion
Thus, the magnitude of the electric field in the region between the plates is:
E=σϵ0
The electric field E due to a single infinite plane sheet of charge with surface charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
For the positive plate with charge density +σ:
- The electric field E1 due to this plate is directed away from the plate (upward if we consider the positive plate on the bottom):
E1=σ2ϵ0
- The electric field E2 due to this plate is directed towards the plate (downward if we consider the negative plate on the top):
E2=σ2ϵ0
In the region between the plates, the electric fields due to both plates add up because they are in the same direction (from the positive plate to the negative plate):
Etotal=E1+E2=σ2ϵ0+σ2ϵ0=σϵ0
Thus, the magnitude of the electric field in the region between the plates is:
E=σϵ0
Topper's Solved these Questions
Similar Questions
Two large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is

View SolutionShow that the force on each plate of a parallel plate capacitor has a magnitude equal to 12QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor 12.
View Solution
Knowledge Check
Two infinitely long parallel sheets having surface charge densities +σand−σ respectively are separated by a small distance. The electric field in the region between the plates is
A0Bσ2∈0Cσ∈0D2σ∈0The energy density in a parallel plate capacitor is given as 2.1 × 10–9 J/m3. The value of the electric field in the region between the plates is :
A2.1NC−1B21.6NC−1C72NC−1D8.4NC−1Three non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
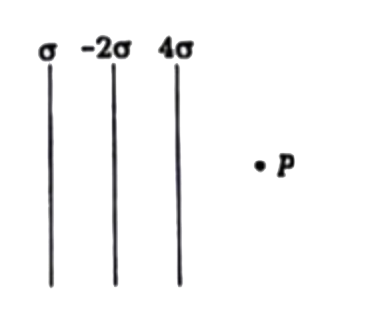 Aσε0Bσ2ε0C3σ2ε0D3σε0
Aσε0Bσ2ε0C3σ2ε0D3σε0
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to (½)QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor ½.
View SolutionTwo large parallel metal plates are 1.5 cm apart and have charges of equal magnitudes but opposite signs on their facing surfaces. Take the potential of the negative plate to be zero. If the potential halfway between the plates is then +10.0V, what is the electric field in the region between the plates?
View SolutionThe plates of a parallel plate capacitor are, not exactly parallel. The surface charge density therefore :
View SolutionThe plates of a parallel plate capacitor are, not exactly parallel. The surface charge density therefore :
View SolutionTwo infinitely long. Parallel, thin sheets, having surface charge densities +σand−σ respectively are separated. By a small distance. The medium between the sheets is vacuum. The electric field in the region between the sheets is
View Solution
