Question

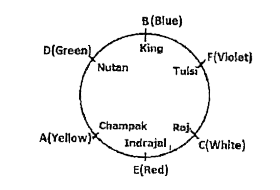
दी गई जानकारी का ध्यानपूर्वक अध्ययन कीजिए और नीचे दिए गए प्रश्नों के उत्तर दीजिए -
छह विद्यार्थी अर्थात् A, B, C, D, E और F एक पुस्तकालय में वृताकार मेज के चारों ओर केंद्र की ओर उन्मुख होकर बैठे हैं। वे भिन्न कॉमिक्स पढ़ते हैं जैसे इंद्रजाल, राज, किंग, नूतन, चंपक और तुलसी लेकिन आवश्यक नहीं कि क्रम समान हो। वे भिन्न रंगों की टीशर्ट पहने हुए हैं जैसे: सफ़ेद, बैंगनी, हरी, लाल, पीली और नीली लेकिन आवश्यक नहीं कि क्रम समान हो। वे विद्यार्थी जो इंद्रजाल, किंग और चंपक पढ़ते हैं न तो सफ़ेद और न ही बैंगनी शर्ट पहने हुए हैं। वे विद्यार्थी जिन्होंने हरी और पीली रंग की टीशर्ट पहनी है न तो इंद्रजाल और न ही किंग कॉमिक्स पढ़ते हैं। A ने तो सफ़ेद टीशर्ट पहनी हुई है न ही वह नूतन पढ़ने वाले व्यक्ति के ठीक बाएँ बैठा है। केवल वह विद्यार्थी जो E और F के मध्य बैठा है वह राज कॉमिक पढ़ता है। वह विद्यार्थी जो सफ़ेद टीशर्ट पहने हुए व्यक्ति के ठीक बाएँ बैठा है, तुलसी कॉमिक नहीं पढ़ता है। D, नूतन कॉमिक पढ़ता है एवं उसकी टीशर्ट का रंग हरा है, यह उस व्यक्ति की ओर उन्मुख है जो राज कॉमिक पढ़ता है। वह विद्यार्थी जो इंद्रजाल पढ़ता है, उस विद्यार्थी के विपरीत बैठा है जिसने नीली टीशर्ट पहनी है, जबकि वह विद्यार्थी जिसने हरी रंग की टीशर्ट पहनी है, चंपक कॉमिक पढ़ने वाले व्यक्ति के ठीक बाएँ बैठा है। तुलसी कॉमिक पढ़ने वाला व्यक्ति, सफ़ेद टी-शर्ट पहने व्यक्ति के ठीक दाएं बैठा है लेकिन किंग कॉमिक पढ़ने वाले व्यक्ति के ठीक बाएँ बैठा है। C, किंग कॉमिक नहीं पढ़ता, जबकि F, इंद्रजाल कॉमिक नहीं पढ़ता है।
निम्न में से कौन चंपक कॉमिक पढता है?

Options

A. A
B. B
C. C
D. E

Answer

A

Explanation