An archery target has three regions formed by three concentric circles in Fig. 12.73. If the diameters of the concentric circles are in the ratio 1:3:5. then find the ratio of the areas of three regions. 
The correct Answer is:1:3:5
Step by step video & text solution for An archery target has three regions formed by three concentric circles in Fig. 12.73. If the diameters of the concentric circles are in the ratio 1:3:5. then find the ratio of the areas of three regions. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
find of the An archery target has three regions formed by three concentric circles as shown in Fig 15.8. If the diameters of the concentric circles are in the ratio 1:2:3. , then find the ratio of the areas of three regions Fig. 15.8
View Solutionfind of the An archery target has three regions formed by three concentric circles as shown in Fig 15.8. If the diameters of the concentric circles are in the ratio 1:2:3. , then find the ratio of the areas of three regions Fig. 15.8
View Solution
Knowledge Check
The circumferences of two circles are in the ratio 3:4. Find the ratio of their areas.
A9:16B16:9C6:9D9:6
If the diameters of the concentric circles shown in the figure below are in the ratio 1:2:3 then find the ratio of the areas of three regions.

View SolutionThe circumference of two circles are in the ratio 2 :3 . Find the ratio of their areas.
View SolutionThe circumferences of two circles are in the ratio 2:3. Find the ratio of their areas.
View SolutionDraw three concentric circles with different radii.
View SolutionThe diameters of two circles are 3.5cm and 6cm .Find the ratio of the area of the larger circle smaller circle.
View SolutionIn the give figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
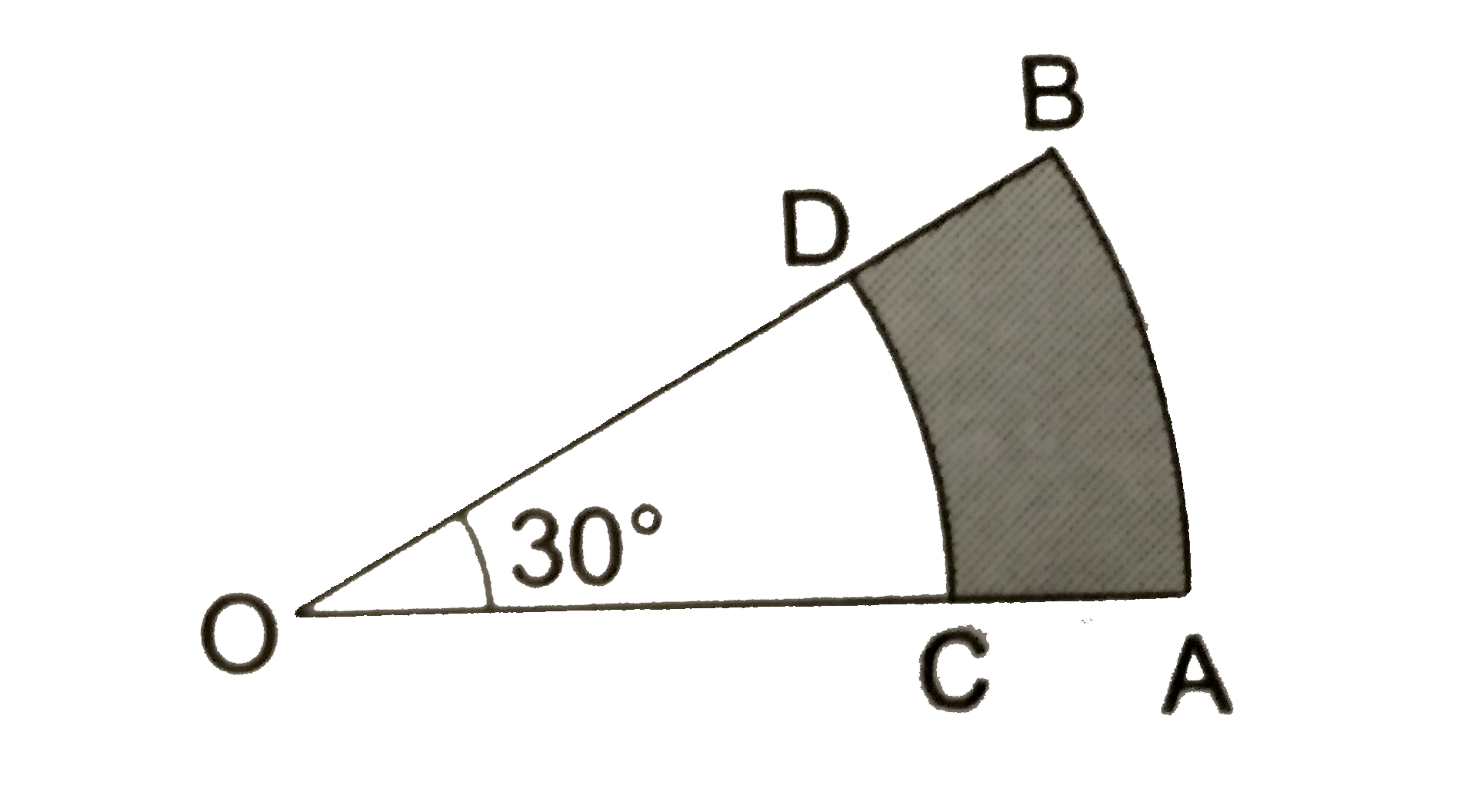
View SolutionThe ratio of the radius of two circles is 4:5. Find the ratio of their areas.
View Solution
