A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
Major sector
The correct Answer is:28.5 cm2
To find the area of the major sector of a circle with a radius of 10 cm that subtends a right angle (90 degrees) at the center, we can follow these steps:
1. Identify the radius and angle:
- Given the radius r=10 cm.
- The angle subtended at the center θ=90∘.
2. Calculate the area of the entire circle:
- The formula for the area of a circle is:
Area=πr2
- Substituting the radius:
Area=π(10)2=100π cm2
3. Calculate the area of the minor sector:
- The area of the sector corresponding to the angle θ is given by:
Area of sector=θ360∘×Area of circle
- Substituting the values:
Area of minor sector=90360×100π=14×100π=25π cm2
4. Calculate the area of the major sector:
- The area of the major sector is the area of the circle minus the area of the minor sector:
Area of major sector=Area of circle−Area of minor sector
- Substituting the areas:
Area of major sector=100π−25π=75π cm2
5. Calculate the numerical value:
- Using π≈3.14:
Area of major sector≈75×3.14=235.5 cm2
Final Answer:
The area of the major sector is approximately 235.5 cm2.
---
- Given the radius r=10 cm.
- The angle subtended at the center θ=90∘.
- The formula for the area of a circle is:
Area=πr2
- Substituting the radius:
Area=π(10)2=100π cm2
- The area of the sector corresponding to the angle θ is given by:
Area of sector=θ360∘×Area of circle
- Substituting the values:
Area of minor sector=90360×100π=14×100π=25π cm2
- The area of the major sector is the area of the circle minus the area of the minor sector:
Area of major sector=Area of circle−Area of minor sector
- Substituting the areas:
Area of major sector=100π−25π=75π cm2
- Using π≈3.14:
Area of major sector≈75×3.14=235.5 cm2
The area of the major sector is approximately 235.5 cm2.
Similar Questions
Knowledge Check
A chord of circle of a radius 28 cm subtends a right angle at the centre. What is the area of the minor sector?
A621cm2B616cm2C718cm2D721cm2
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
(i) minor segment
(ii) major sector.
View SolutionA chord of a circle of radius 14 cm makes a right angle at the centre. Find the area of the sector.
View SolutionA chord of a circle of radius 15 cm subtends an angle of 60∘ at the centre . Find the areas of the corresponding minor and major segments of the circle.
View SolutionThe chord of a circle of radius 8 cm subtends a right angle at its centre. Find the length of the chord.
View SolutionA chord of a circle of radius 12 cm subtends an angle of 120∘ at the centre . Find the area of the corresponding segment of the circle.
View SolutionA chord of a circle of radius 12 cm subtends an angle of 60° at the centre. Find the area of the corresponding segment of the circle.
( Use π=3.14,√3=1.73 )
View SolutionA chord of a circle of radius 12 cm subtends an angle of 120∘ at the centre.
Find the area of the corresponding segment of the circle (Use π=3.14 and √3=1.73)
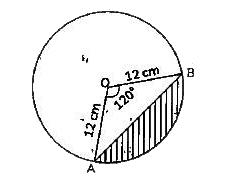
View Solution
