A rod AB of length 2m is hinging at point A and its other end B is attached to a platform on which a point of mass m is kept. Rod rotates about point A maintain angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the platform (g=10ms−2)
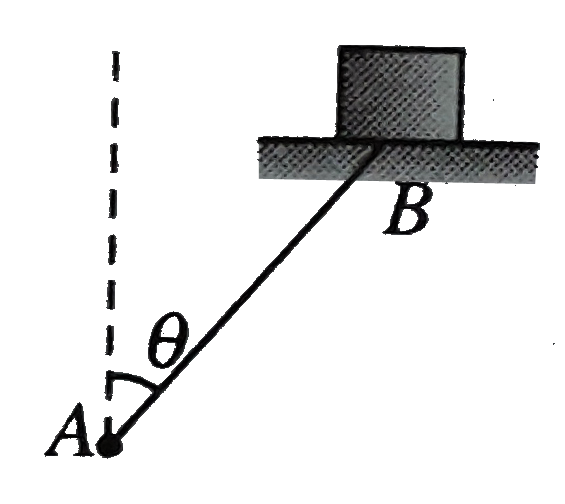
The correct Answer is:01.00
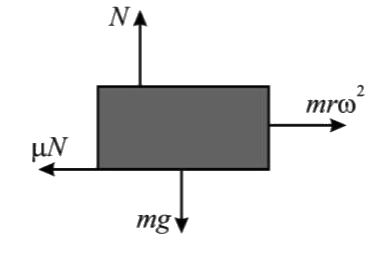
N=mg,μN=meω2
μmh=m2sinθω2
⇒ ω=√μθ2sinθ=√0.1×102×sin20
=1rads−1
Topper's Solved these Questions
Similar Questions
A rod AB of length 2m is hinging at point A and its other end B is attached to a platform on which a point of mass m is kept. Rod rotates about point A maintain angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the platform (g=10ms−2)

View SolutionA rod AB of length 2m is hinging at point A and its other end B is attached to a platform on which a point of mass m is kept. Rod rotates about point A maintain angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the platform (g=10ms−2)

View Solution
Knowledge Check
Two blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform. The coefficient of friction between the platform and the two blocks is the same. The platform moves with an acceleration. The force of interaction between the blocks is :
 Azero only if m1=m2Bzero in all casesCnon - zero only if m1>m2Dnon - zero only if m1<m2
Azero only if m1=m2Bzero in all casesCnon - zero only if m1>m2Dnon - zero only if m1<m2A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
What is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
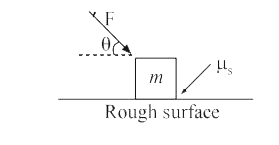
View SolutionA body of mass m rests on a horizontal rough platform. Coefficient of static friction is u. Calculate the minimum possible force required to move the body along the platform.
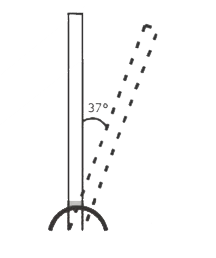
View SolutionA uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
View SolutionA rod is kept inclined at an angle θ with the horizontal A sleeve of mass m can slide on the rod. If the coefficient of friction between the rod and the sleeve is μ, for what values of horizontal acceleration a of the rod, towards left, the sleeve will not slide over the rod?
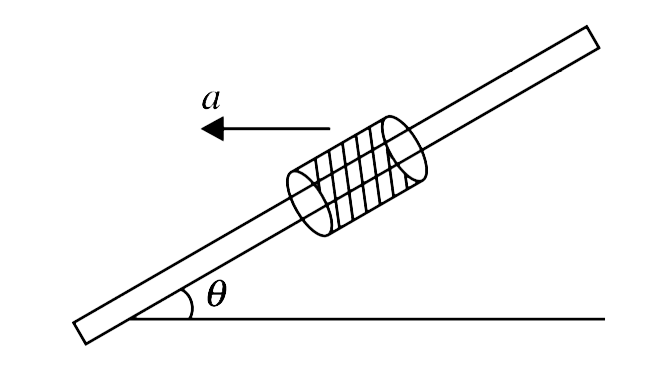
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:

View Solution

