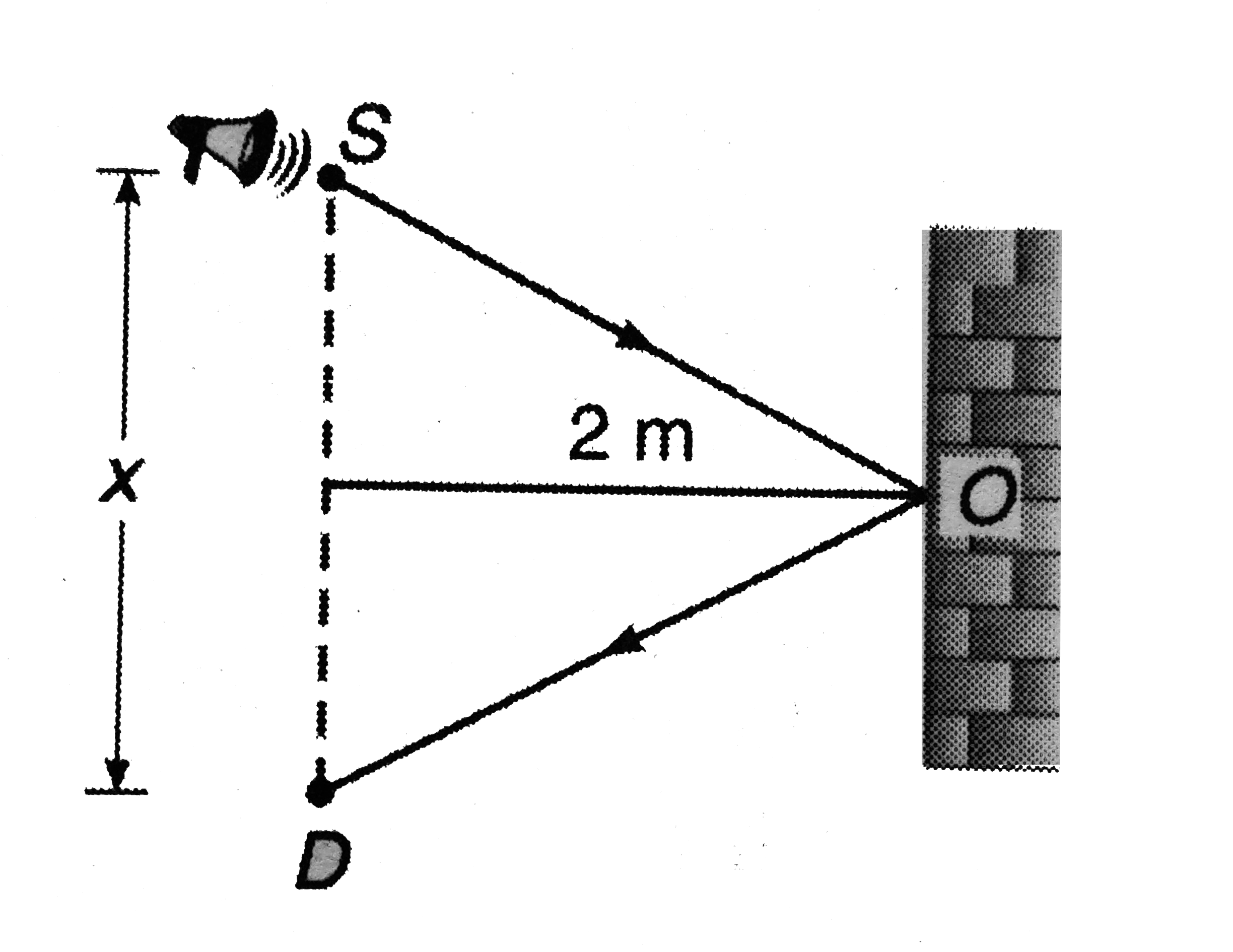
A source emitting sound of frequency 100 Hz . It is placed in front of a wall at a distance of 2m from it. Also, if a detector is also placed in front of the wall at the same distance from it, then the minimum distance between the source and the detector for which detector detects a maximum of sound is
________ m(vsound=360m/s)
The correct Answer is:00.42
To solve the problem step by step, we will analyze the situation involving the sound source, the wall, and the detector.
Step 1: Understand the Setup
We have a sound source emitting sound at a frequency of 100 Hz, placed 2 m away from a wall. A detector is also placed 2 m away from the wall. We need to find the minimum distance x between the source and the detector for which the detector detects a maximum of sound.
Step 2: Calculate the Wavelength
The speed of sound v is given as 360 m/s. The wavelength λ can be calculated using the formula:
λ=vf
where f is the frequency of the sound. Substituting the values:
λ=360m/s100Hz=3.6m
Step 3: Determine Path Difference for Maximum Sound
For the detector to detect a maximum sound, the path difference Δx between the direct sound path and the sound reflected off the wall must be an integer multiple of the wavelength:
Δx=nλ(n=0,1,2,…)
For the first maximum, we take n=1:
Δx=λ=3.6m
Step 4: Analyze the Path Lengths
Let x be the distance between the source and the detector. The total distance traveled by the sound from the source to the wall and then to the detector is:
Distance via wall=2+2+x=4+x
The direct distance from the source to the detector is simply x.
Step 5: Set Up the Equation for Path Difference
The path difference is given by:
Δx=(4+x)−x=4m
We need this path difference to equal 3.6m:
4=n⋅3.6
Solving for n:
n=43.6≈1.11
Since n must be an integer, we can check for n=1 and n=2.
Step 6: Solve for Minimum Distance
Using n=1:
Δx=3.6m
Setting up the equation:
4+x−x=3.6
This simplifies to:
4=3.6+x
Thus:
x=4−3.6=0.4m
Step 7: Conclusion
The minimum distance between the source and the detector for which the detector detects a maximum of sound is:
0.4m
We have a sound source emitting sound at a frequency of 100 Hz, placed 2 m away from a wall. A detector is also placed 2 m away from the wall. We need to find the minimum distance x between the source and the detector for which the detector detects a maximum of sound.
The speed of sound v is given as 360 m/s. The wavelength λ can be calculated using the formula:
λ=vf
where f is the frequency of the sound. Substituting the values:
λ=360m/s100Hz=3.6m
For the detector to detect a maximum sound, the path difference Δx between the direct sound path and the sound reflected off the wall must be an integer multiple of the wavelength:
Δx=nλ(n=0,1,2,…)
For the first maximum, we take n=1:
Δx=λ=3.6m
Let x be the distance between the source and the detector. The total distance traveled by the sound from the source to the wall and then to the detector is:
Distance via wall=2+2+x=4+x
The direct distance from the source to the detector is simply x.
The path difference is given by:
Δx=(4+x)−x=4m
We need this path difference to equal 3.6m:
4=n⋅3.6
Solving for n:
n=43.6≈1.11
Since n must be an integer, we can check for n=1 and n=2.
Using n=1:
Δx=3.6m
Setting up the equation:
4+x−x=3.6
This simplifies to:
4=3.6+x
Thus:
x=4−3.6=0.4m
The minimum distance between the source and the detector for which the detector detects a maximum of sound is:
0.4m
Topper's Solved these Questions
Similar Questions
(a) A source of sound S and a detector D are placed at some distance from one another. A big cardboard is placed near the detector and perpendicular to the line SD as shown in figure. It is gradually moved away and it is found that the intensity changes from a maximum to a minimum as the board is moved through a distance of 20cm. Find the frequency of the sound emitted. Velocity of sound in are is 336m/s.

(b) A source emitting sound of frequency 180Hz is placed in front of a wall at a distance of 2m from it. A detector is also placed in front of the wall at the same distance from it. find the minimum distance between the source and the detector for which the detector detects a maximum of sound . Speed of sound in air =360m/s.
View SolutionA source emitting sound of frequency 180 Hz is alced in front of a wall at a distance of 2 m from it. A detector is also placed in front of the weal at the same distance from it. Find the minimum distance between the source and the detector for which the detector detects a maximum of sound. Speed of sound in air =360ms−1.

View Solution
Knowledge Check
A source emitting sound of frequency 180Hz is placed in front of a wall at distance of 2m from it . A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detector for which the detector detects a maximum of sound. Speed of sound in air =360m/s.
A3mB2mC3/2mDzeroA soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
A4mB3 mC1 mD2mThe minimum distance between source of sound and reflection surface for the clear hearing of sound is
A17 mB1.7 mC20 mD19.2 m
A source of sound emitting waves at 360HZ is placed in front of a vertical wall, at a distance 2m from it. A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detestor for which the detector detects a maximum of sound. Take speed of sound in air=360m/s. Assume that there is not phase change in reflected wave.
View SolutionA source emitting sound of frequency 165Hz is placed in frount of a wall at a distance of 2m from it. A detector is also placed in fornt of the wall at the same distance from it. Find the distance between the source and the detector for which the detector detects phase difference of 2π between the direct and reflected wave. Speed of sound in air =330m/s.
View SolutionWhat is the minimum distance of the obstacle from the source of sound for hearing distinct echo ?
View Solutionthe minimum distance between the reflecting surface and source for listening the eco of sound is ( take speed of sound 340ms)
View SolutionTo hear distinct echoes, the minimum distance of the obstacle from the source of sound must be ______ .
View Solution

