an inductor of inductance 2.00 H is joined in series with a resistor of resistance 200Ω and a battery of emf 2.00 V. At t = 10 ms, find (a) th current in the circuit, (b) the power delivered by the batter, (c ) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.Solution in Gujrati
Here L=2H,R=200W,
E=2V,t=10ms
(a)i=i0(1−e−t/(τ))
=2200(1−e−10×10−8×2002)
=0.01(1−e−1)
0.01×0.632=6.3mA
(b) Power delivered by the battery
P=Vi
P=Ei0(1−e−t/(τ))
P=2×2200(1−e10×10−3×2002)
P=0.02(1−e−1)
=0.01264=12mW.
(c)Powerdissipated∈theresis→r=i2R
=[i_(0)(1-e^(-t//(tau)))]^(2) R<br>=(6.3xx6.3xx200xx10^(-5))<br>=79.38xx10^(-4)<br>=7.938xx10^(-3)=8mW.<br>(d)Rateatwhiche≠rgyiss→red∈themag≠ticfield=(12)(Li2)
=(L2)(i0)2(1−e−t/(τ))2
=2xx10^(-2)(0.225)<br>=0.455xx10^(-2)<br>=4.6×10−3
=4.6mW.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
Shown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
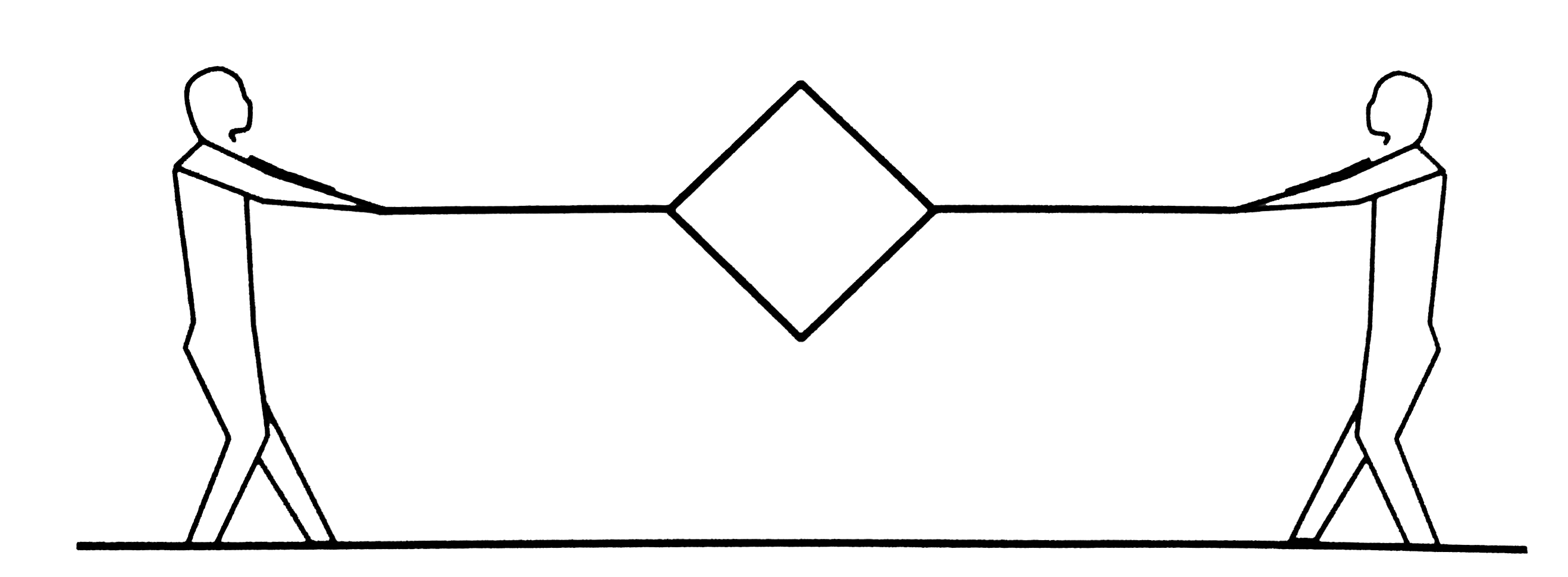07:16View SolutionA bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
04:13View SolutionFind the dimensional formula of ε0 .
10:05View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
04:17View SolutionA capacitor of capacitance 12(μ)Fis connected to a battery of emf 6.00V and internal resistance 1.00(Ω)through resistanceless leads. 12.0(mu)s after the connections are made, what will be (a) the current in the circuit, (b)the power delivered by the battery ,(c)the power dissipated in heat and (d)the rate at which the energy stored in the capacitor is increasing.
06:19View SolutionAn inductor of inductance 5.0 H, having a negligible resistance, is connected in series with a 100Ω resistor and a battery of emf 2.0 V. Find the potential difference across the resistor 20 ms after the circuit is switched on.
04:12View Solutionan inductor of inductance 2.00 H is joined in series with a resistor of resistance 200Ω and a battery of emf 2.00 V. At t = 10 ms, find (a) th current in the circuit, (b) the power delivered by the batter, (c ) the power dissipated in heating the resistor and (d) the rate at which energy is being stored in magnetic field.
08:44View SolutionResistors P,Q,andR in the circuit have equal resistances. If the battery is supplying a total power of 12W , what is the power dissipated as heat in resistors R?
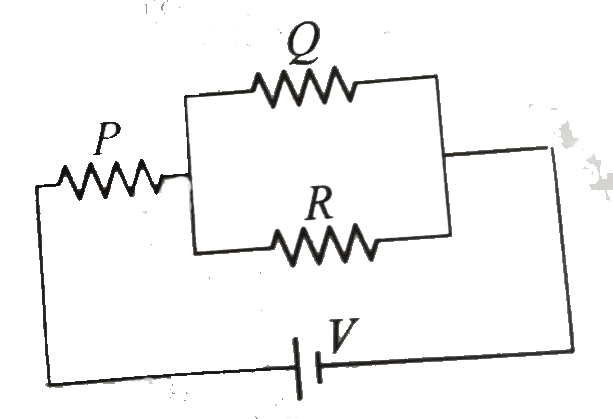02:06View SolutionA series battery of 10 lead accemulators each of emf 2V and internal resistor 0.25 ohm charged by a 220V d.c. mains. To limit the charging circuit a resistance of 47.5Ω is used in series in the charging circuit. What is (a) the power applied by the mains and (b) power dissipated as heat ?
(c) Account for the difference of power in (a) and (b)View SolutionA capacitance C , a resistance R and an emf E are connected in series at t=0 what is the maximum value of (a) the potential differnece across the resistor, (b) the current in the circuit , (c ) the power delivered by the battery. (d) the power converted into heat, (e) the potential differnece across the capicitor and (f) the energy stored in the capacitor.
01:18View SolutionA3 H inductor is placed in series with 10 Omega resistor and an emf of 10V is applied to the combination. Find (i) the current at 0.3s, (ii) the rate of increase of current at 0.3s, (iii) the rate at which energy is dissipated as heat at t = 0.3s . (iv) the rate at which energy is stored in the magnetic field at 0.3s. (v) the rate at which energy is delivered by the battery, and (vi) the energy stored when the current has attained steady value.
11:11View SolutionA inductor of 20mH inductance and a resistor of 100 Omega resistance are connected in series to a battery of emf 10V. After a long time the circuit is short-circuited and the battery is disconnected. Find the current in the circuit 1 ms after short-circuiting.
04:46View Solution5 A 50 mH inductor is in series with a 10 2 resistor and a battery with an emf oj 25 V. At t = 0 the switch is closed. Find Q(d) the power dissipated in the resistor
09:24View SolutionAn inductor of inductance L and resistor R are joined together in series and connected by a source of frequency omega . The power dissipated in the circuit is
04:42View SolutionAn inductor of self-inductance L and resistor of resistance R are connected in series to a battery of emf E and negligible resistance.Calculate the maximum rate at which energy is stored in the inductor.
View SolutionA battery has an emf of 12 V and connected to a resistor of 3Ω. The current in the circuit is 3.93 A. Calculate (a) terminal voltage and the internal resistance of the battery (b) power delivered by the battery and power delivered to the resistor.
03:59View Solution