An inductance L and a resistance R are connected in series with a battery of emf e. Find the maximum rate at which the energy is stored in the magnetic field.Solution in Gujrati
The energy stored in the magnetic field at tiem t is U=12Li2=12Li20(1−e9−tτ)2
The rate at which the energy is stored is P=dUdt=Li20(1−e−tτ(−e−tτ)(−1τ) =Li20τ(e−tτ−e−2tτ
This rate will be maximum when (dP)/(dt) = 0 or, (Li_0^2)/(tau) (-(1)/(tau)e^(-t/tau)+(2)/(tau)e^(-2t/tau)) = 0or,e^(-1=t/tau) = (1)/(2)pu∈g∈(i),P_max = (Li_0^2)/(tau)((1)/(2) - (1)/(4))=(Lepsilon^2)/(4R^2(L/R) = (epsilon^2)/(4R)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Short Answer
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 1
12 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
A metallic loop is placed in a nonuiform steady magnetic field. Will an emf be induced in the loop?
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
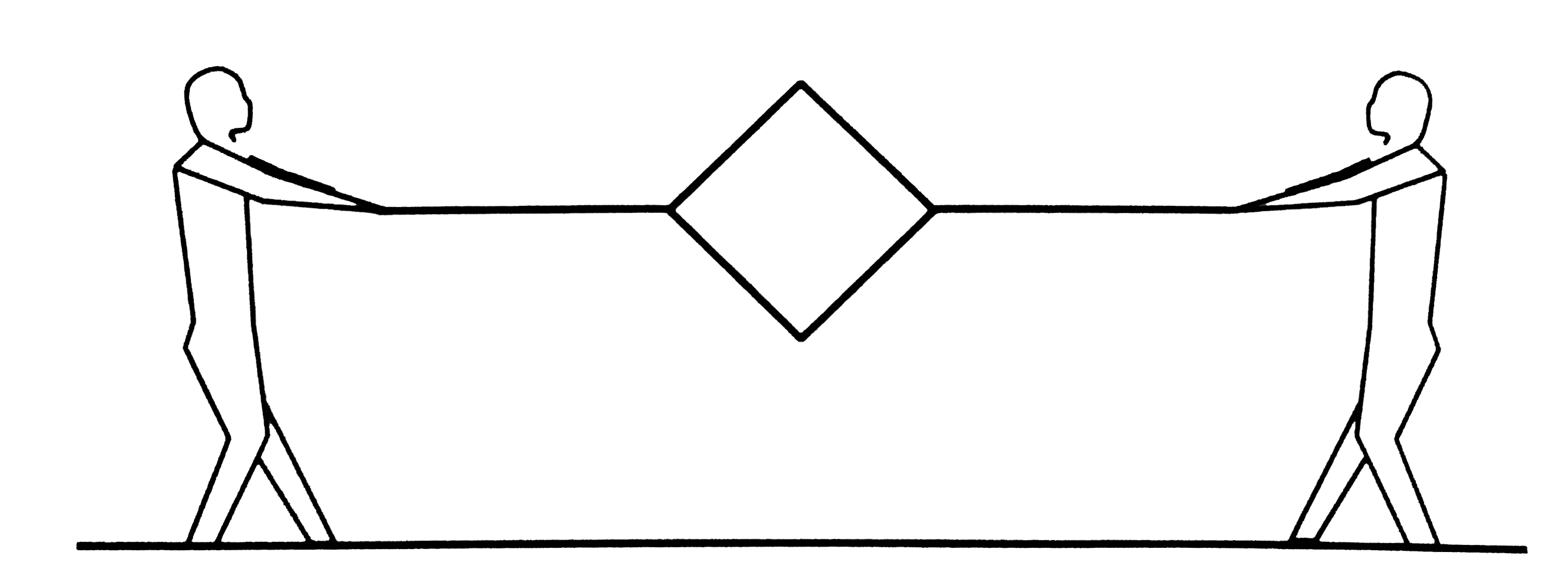
View SolutionShown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionA capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View SolutionAn inductance L and a resistance R are connected in series with a battery of emf epsilon. Find the maximum rate at which the energy is stored in the magnetic field.
View SolutionA coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before (a) the current reaches half its maximum value, (b) the power dissipated in heat reaches half its maximum value and © the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionA coil having an inductance L and a resistance R is connected to a battery of emf E . Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value.
View SolutionAn LR series circuit has L=1 H and R=1 Omega .It is connected across an emf of 2 V .The maximum rate at which energy is stored in the magnetic field is:
View Solutionएक प्रेरक L तथा प्रतिरोध R वि. वा. ब. ε की बैटरी से श्रेणी क्रम में जुड़े हैं | चुंबकीय क्षेत्र में ऊर्जा संचित होने की अधिकतम दर है
View SolutionWhat is the maximum rate at which energy is stored in inductor (L) when it is connected in series with resistance R and one battery of emf E and negligible internal resistance? Refer to growth and decay of current in a coil, explained in competition file.
View SolutionAn inductor of self-inductance L and resistor of resistance R are connected in series to a battery of emf E and negligible resistance.Calculate the maximum rate at which energy is stored in the inductor.
View SolutionA capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View SolutionAn inducatane L and a resistance R are connected in series with a battery of emf epsilon. Find the maximum rate at which the energy is stored in the magnetic field.
View SolutionA capacitor of capacitance C is connected to a battery of emf E at t = 0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View Solution
