A conducting circular loop of face are is placed perpendicular to a magnetic field which varies as 10 Omega, find the thermal energy developed in the loop in this period.Solution in Gujrati
The face area of the loop is Phi =B_0 A sin omega tverepsilon =-(dPhi)/(dt) =- B_0 Aomega cos omega t
the current is i= (varepsilon)/(R)=-(B_0 A omega)(R) cos omega t =- i_0 cos omega t
The current changes sinusoidally with the time period Q=int_0^T idt=-i_0 int_0^T cos omega t dt
(b)The thermal energy produced in 40 ms is =(i_0^2 RT)/(2) =(B_0^2 A^2 omega^2)/(2R^2) R((2pi)/(omega)) = (piB_0^2A^2 omega)/(R) =(pi X(0
20T)^2 X(2
5 X10^(-3)m^2)2 X(50pi s^(-1))/(10 Omega) =1
25X10^(-5) J
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:HC VERMAChapter:ELECTROMAGNETIC INDUCTIONExercise:Short Answer
Explore 13 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMAChapter:ELECTROMAGNETIC INDUCTIONExercise:Objective 1
Explore 12 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMAChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE
Explore 9 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMAChapter:ELECTRIC FIELD AND POTENTIALExercise:Exercises
Explore 75 Videos
- ELECTROMAGNETIC WAVESBook:HC VERMAChapter:ELECTROMAGNETIC WAVESExercise:Exercises
Explore 9 Videos
Similar Questions
A metallic loop is placed in a nonuiform steady magnetic field. Will an emf be induced in the loop?
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
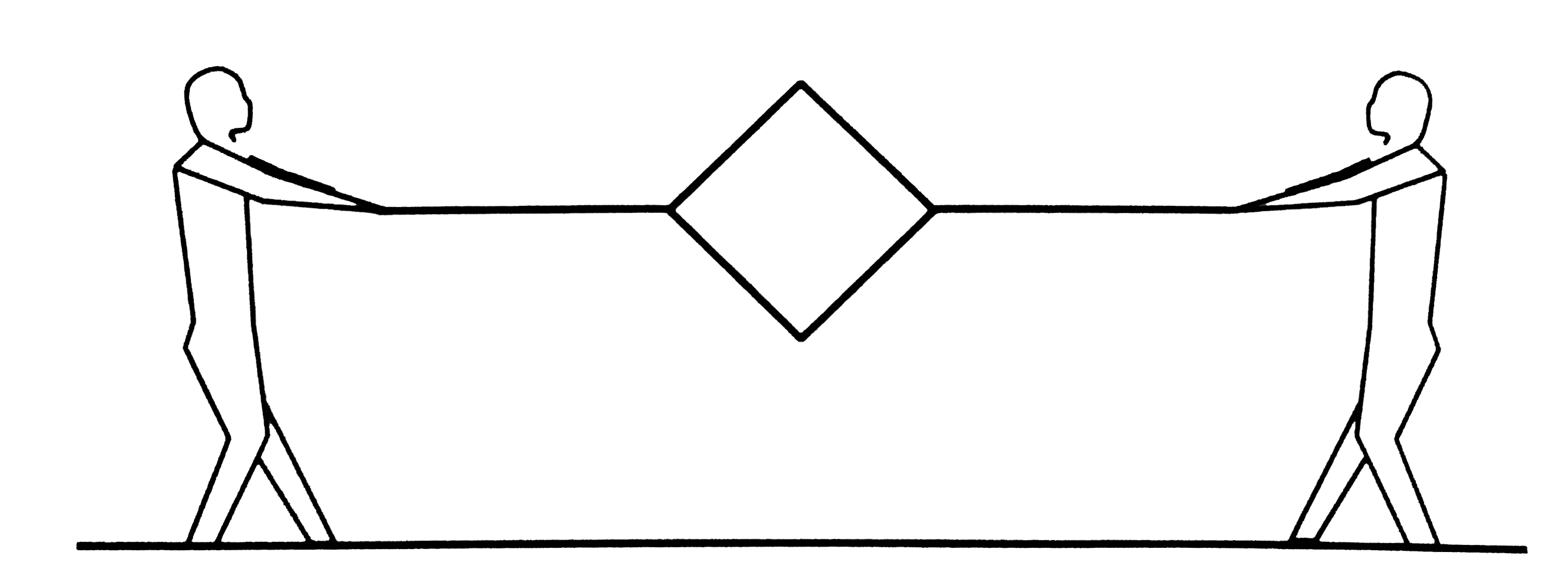
View SolutionShown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionA conducting circular loop of face are 2.5X10−3m2 is placed perpendicular to a magnetic field which varies as B=(0.20T)sin[(50πs−1)t].(a)F∈dthechar≥jflow∈gthroughanycross−sectiondur∈gthetimet=0→t=40ms.(b)Iftheresistanceofthel∞pis10 Omega, find the thermal energy developed in the loop in this period.
View SolutionA loop of wire enclosing an area S is placed in a region where the magnetic field is perpendicular to the plane. The magnetic field B varies with time according to the expression B=B_0e^(-at) where a is some constant. That is, at t= 0 . The field is B_0 and for t gt 0 , the field decreases exponentially. Find the induced emf in the loop as a function of time.
View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.
View SolutionA circular brass loop of radius a and resistance R is placed with it plane perpendicular to a magnetic field, which varies with time as B=B0sinωt. Obtain the expression for the induced current in the loop.
View SolutionA conducting loop of cross-area A and resistance R is placed perpendicular to a magnetic field B . The loop is withdrawn completely from the field. The change, which flows through any cross-section of the wire in the process
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B = B_0e^(-t//tau) , where B_0 and tau are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t to oo) is :
View SolutionA circular conducting loop of area 100 cm^(2) and resistance 3 Omega is placed in a magnetic field with its plane perpendicular to the field. If the field is spatially uniform but varies with time t (in second) as B(t) = 1.5 cos omega t tesla, the peak value of the current in the loop is
View SolutionA conducing circular loop of area 2.5xx10^(-3)m^(2) and resistance 10Omega is placed perpendicular to a uniform time varying magnetic field B(t)=0.6 sin(50pit)T . What is the net charge (in mC) flowing through the loop during t = 0 and t = 10 ms ?
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B = gamma t is applied perpendicular to plane of the loop where gamma is constant and t is time. The induced current flowing through loop is
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View Solution