Sound with intensity larger than 120 dB appears painful to a person. A small speaker delivers 2.0 W of audio output. How close can the person get to the speaker without hurting his ears ?Solution in Gujrati
The correct Answer is:C, D
If sound level =120 dB,
then I=∫ensity=1Wm2
Let the closet distance be x.
So,Intensity=(2/(4pix^2))=1<br>rarr x^2(2/(4pi))<br>rarr x=40cm
Similar Questions
A microphone of cross sectional area 0.80cm2is placed in front of a small speaker emitting 3.0 W of sound output. If the distance between the microphone and the speaker is 2.0 m how much energy falls on the microphone in 5.0 s?
View SolutionSound with intensity larger than 120 dB appears painful to a person. A small speaker delivers 2.0 W of audio output. How close can the person get to the speaker without hurting his ears ?
View SolutionA small speaker delivers 2 W of audio will one detect 120 dB intensity sound ? [Given reference intensity of sound as 10^(-12) W//m^(2) ]
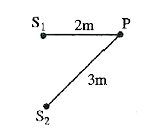
View SolutionTwo idential speakers emit sound waves of frequency 660Hz uniformly in all directions. The audio output of each speaker is lmW and the speed of sound in air. A point P is a distance 2m from one speaker and 3m frorr the other. If they are driven coherently but out of phase by 180°. the intensity at the point .P. is:
View SolutionSound with intensity larger than 120 dB. appears painful to a person. A small speaker delivers 4W of audio output. How close can the person get to the speaker without hurting his ears?
View Solution(a) What is the intensity of a 60 dB sound ? (b) If the sound level is 60 dB close to a speaker that has an area of 120 cm ^(2) . What is the acoustic power output of the speaker?
View SolutionThe power of sound from the speaker of radio is 10 W. Now, the power of sound from the speaker of the radio is increased to 400 W by increasing the volume of the radio. The power increased in dB as compared to original power is nearly
View SolutionThe power of sound from the speaker of the radio is 10 W. Now, the power of the sound from the speaker of the radio is increased to 400 W by increasing the volume of the radio. The increase of power in dB compared to the initial power is approximately:
View Solution
