Find∫6x(x2+6)dx.
a)3x42+18x2+C
b)3x42−18x+C
c)3x42−18x2+C
d)3x42+x2+CSolution in Gujrati
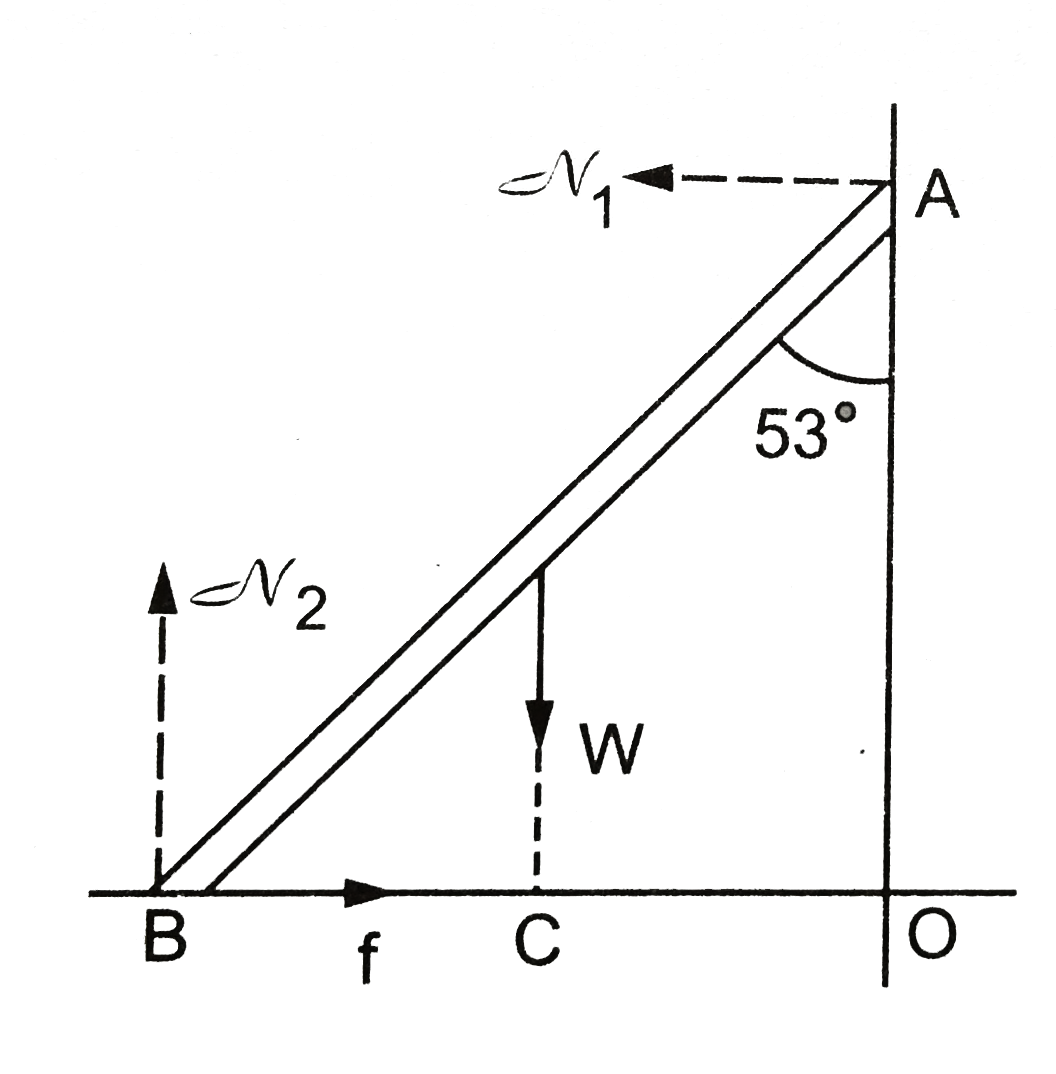
The force acting on the ladder are shown in ure. They are
a. its weight W
b. normal force N1 by the vertical wall
c. normal force N2 by the floor and
d. frictioN/Al force f by the floor.
Taking horizontal and vertical components
N1=f.............i
N2=W...........ii
Taking torque about B
N1(AO)=W(CB)
or,N1(AB)cos530=WAB2sin530
or, N135=W245
orN=23W.....iii
The normal force by the floor is
N2=W(10kg)(9.8ms2)=98N.
The frictioN/Al force is
f=N1=23W=65N
Similar Questions
If a(x)=b(x)+c(x), where b(x)=3x2−8x+113 and c(x)=−3x2+18x+7 and x is an integer , than a(x) is always divisible by which of the following ?
View SolutionConsider a=x^(2)+3x+2,b=x^(2)+3x+4,c=x^(2)+3x+8 ; if a, b, c are in HP then product of possible values of x is
View SolutionThe solution of x2+y2dydx=4 is
a. x2+y2=12x+C b. x2+y2=3x+C c. x3+y3=3x+C d. x3+y3=12x+C
View SolutionHow much is −2x2+x+1 less than x2+2x−3?
(a)x2+3x−2 (b) 3x2+x−4 (c)−3x2−x+4 (d) 3x2+3x−4
View SolutionDivide 6x4−9x3+18x2 by 3x
View SolutionLet two numbers have arithmatic mean 9 and geometric mean 4.Then these numbers are roots of the equation (a) x2+18x+16=0 (b) x2−18x−16=0 (c) x2+18x−16=0 (d) x2−18x+16=0
View SolutionEvaluate :
−7x2+18x2+3x2−5x2
View SolutionThe solution of the differential equation dydx+x(x2+3y2)y(y2+3x2)=0 is (a)x4+y4+x2y2=c (b)x4+y4+3x2y2=c (c)x4+y4+6x2y2=c (d)x4+y4+9x2y2=c
View Solution
