The second law of motion, in mathematical form can be written as ____
a) F = dp/dt
b) F = ma
c) F = v(dm/dt)
d) F = mvSolution in Gujrati
Video Solution
Text Solution
The correct Answer is:A, B
The projected velocity =u
The angle of prjection =θ
Whentehprojectilehits the ground for the 1st time,
The velocity would be the same i.e u
Here the component of velocity paralel to ground
ucosθ should remain constant
But teh verticla component of the projectile under goes.
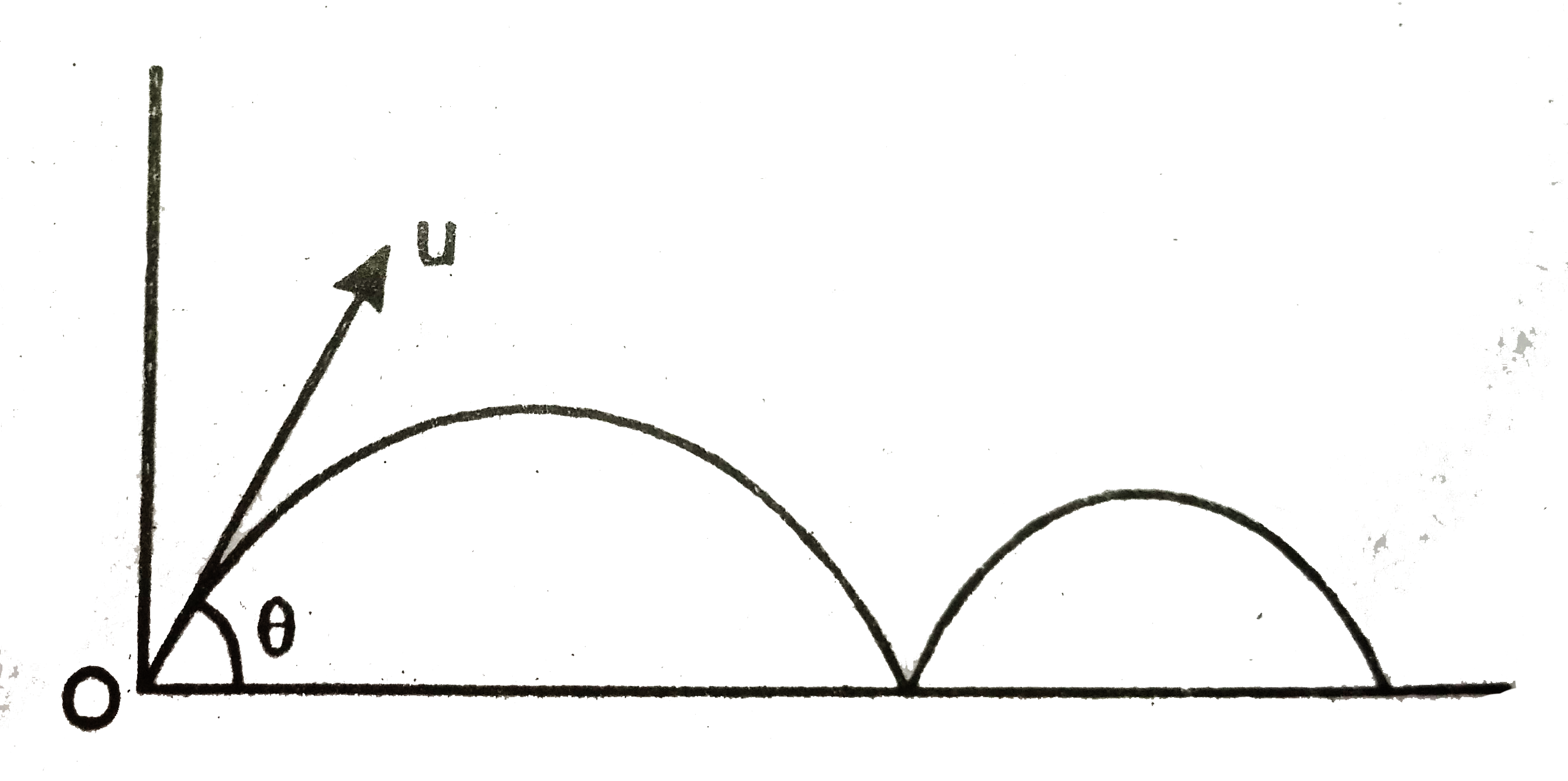
→v=eusinθ
Now for the 2nd projectile motion.
u=velocityofprojection<br>=sqrt((ucostheta)^2+(eusintheta)^2)<br>andAng≤ofprojection<br>=alpha=tan^I-1((eusintheta)/(ucostheta))<br>=tan^-1 (etantheta)<br>or taN/Alpha=etantheta..............2<br>Becausey=xtaN/Alphatan^-1(gx^2sec^2alpha)/(2u^2)............e<br>Here y=0, taN/Alpha<br>=etantheta<br>sec^2alha=1+e^2tan^2theta<br>andu^2=u^2cos^2theta+e^2u^2sin^2theta<br>pu∈gtheabovevalues∈theequation3<br>xetantheta=(gxx^2(1+e^2tan^2theta))/(2u^2(cos^2theta+e^2sintheta))<br>orx=2eu2tanθ(cos2θ+e2sin2θ)g(1+e2tan2θ)
=2eu2tanθ.cos2θg
eu2sin2θg
→So,omthe⋆t∈gp∮Oitwillfasllatadistance<br>(u^2sin2theta)/g+(eu^2.sin2theta)/g<br>(u^2sin2theta)/g(1+e)
|
Similar Questions
If ∫x0f(t)dt=x+∫1xtf(t)dt, then the value of f(1) is
View Solutionf(x)=∫x0f(t)dt=x+∫1xtf(t)dt, then the value of f(1) is
View SolutionShow that force can be expressed as the product of mass and acceleration. [Hint F=(dpdt)−(ddt)mv−m(dvdt)−ma]
View SolutionDerive the mathematical formulation of Newton's second law of motion F = ma.
View SolutionState Newton's second law of motion and hence derive F = Ma.
View SolutionIf ∫x0f(t)dt=x+∫lxtf(t)dt, then the value of f(1) is :
View SolutionLet f be a continuous function on [a,b]. If F(x)=(∫xaf(t)dt−∫bxf(t)dt)(2x−(a+b)), then prove that there exist some c∈(a,b) such that ∫caf(t)dt−∫bcf(t)dt=f(c)(a+b−2c).
View SolutionIf x=f(t)cost−f′(t)sint and y=f(t)sint+f′(t)cost, then (dxdt)2+(dydt)2= f(t)−f(t) (b) {f(t)−f(t)}2 (c) {f(t)+f(t)}2 (d) none of these
View Solution