Which one of the following operations is valid?
a) Vector multiplied by scalar
b) Vector added to scalar
c) Vector subtracted from scalar
d) Vector divided by vectorSolution in Gujrati

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

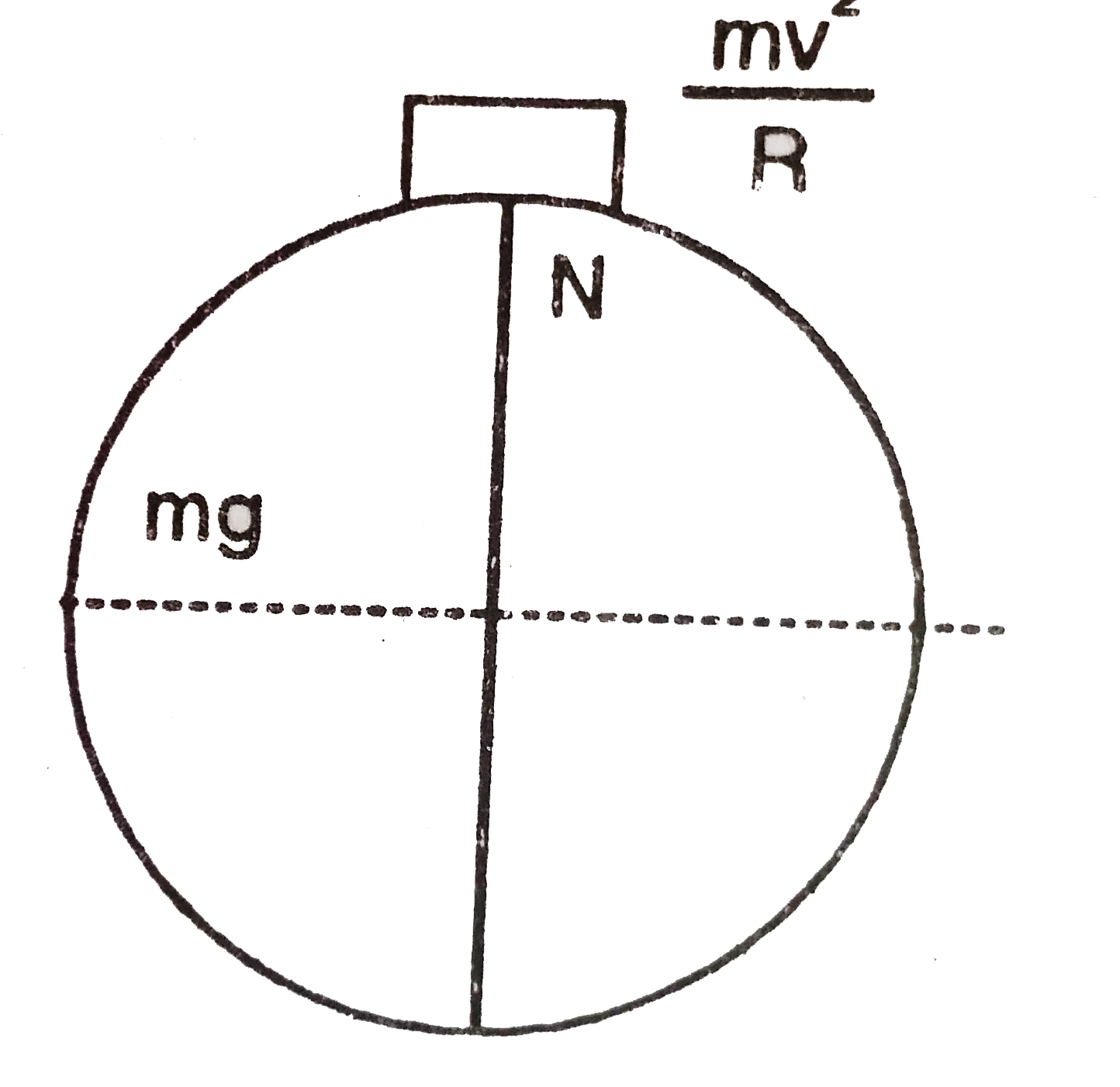
a. Radius =R
Horizontal speed=v
From the free body diagram ure
N=normal force
$= m g - \frac{m v^{2}}{R}$
b. When the particle is givenmaximum velocity so that the centrifugal force balances the weight, the particle does not slip on the sphere,
$\to \frac{m v^{2}}{R} = m g$
$\to v = \sqrt{g R}$
c if the body is given velocity $v_{1}$ at the top such that
$v_{1} = \frac{\sqrt{g R}}{2}$
$v_{1}^{2} = \frac{g R}{4}$ Let the velocity be $v_{2}$ when it leaves contact with the surface, ure

So, (mv_2^2)/R=mgcostheta $< b r >$ rarrv_2^2=Rgcostheta $... ... . . i < b r >$ Again $(\frac{1}{2}) m v_{2}^{2} - (\frac{1}{2}) m v_{1}^{2}$
$= m g R (1 - cos θ)$
$\to v_{2}^{2} = v_{1}^{2} + 2 g R (1 - cos θ)$ ............ii
From equatioon i and equation ii
$R g cos θ = (\frac{R g}{4}) + 2 g R (1 - cos θ)$
$\to cos θ = (\frac{1}{4} + 2 - 2 cos θ)$
$\to 3 cos θ = (\frac{9}{4})$
$\to θ = {cos}^{- 1} (\frac{3}{4})$

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile