A force of 40 N acts on body of mass 5 Kg. What is the amount of work done if the total displacement is 2 m and is in the direction of the force applied?
a) 80 J
b) -80 J
c) 40 J
d) 16 JSolution in Gujrati
ure shows the forces acting on the two blocks. As we aree looking for the maximum value off M/m. the equilibrium is limiting. Hence, the frictioN/Al forces are equal to μ times the corresponding normal forces.

elquilibrium of the block m gives
T=muN_1 and N_1=mg<br>whichgives<br>T=mu mg......i<br>Next,consrtheequilibriumoftheblockM.Tak∈gcompo≠ntsparal≤l→the∈cl∈e<br>T+μN2=Mgsinθ
Taking components normal to the incline
N2=Mgcosθ
These give T=Mg(sinθ−μcosθ)..........ii
From i and i μmg=Mg(sinθ−μcothη)
or, Mm=μsinθ−μcosthhη
tanθ<μ,(sinthet−μcosθ)<0 and the system wil not slide for any value of M/m.
Similar Questions
A constant force of 1 N is applied on an object. The body displaces 1 m in the direction of the force. Then work done is ……………. J
View SolutionA body displaced 10m under the force of 10 N . If the work done on the body is 50 J , then the angle between the force and displacement will be ……..
View Solutionएक पिण्डपर 40 न्यूटन का बल लगाने से वह बल की दिशा में 60∘ के कोण पर 20 मी विस्थापित हो जाता है। बल द्वारा कृत कार्य होगा
View SolutionHow much force is applied on the body when 780 J of work is done in displacing the body through a distance of 30 m in the direction of force?
View SolutionIf change in internal energy -80 J. The work done by system is +40 J. Calculate the heat change.
View SolutionA body of mass 2 kg starts with an intitial-velocity 5 m/s. It the body is acted upon by a time dependent force (F) as shown in figure, then work done on the body in 20 s is
A. − 875 J
B. 875J
C. 600J
D. − 600 N J
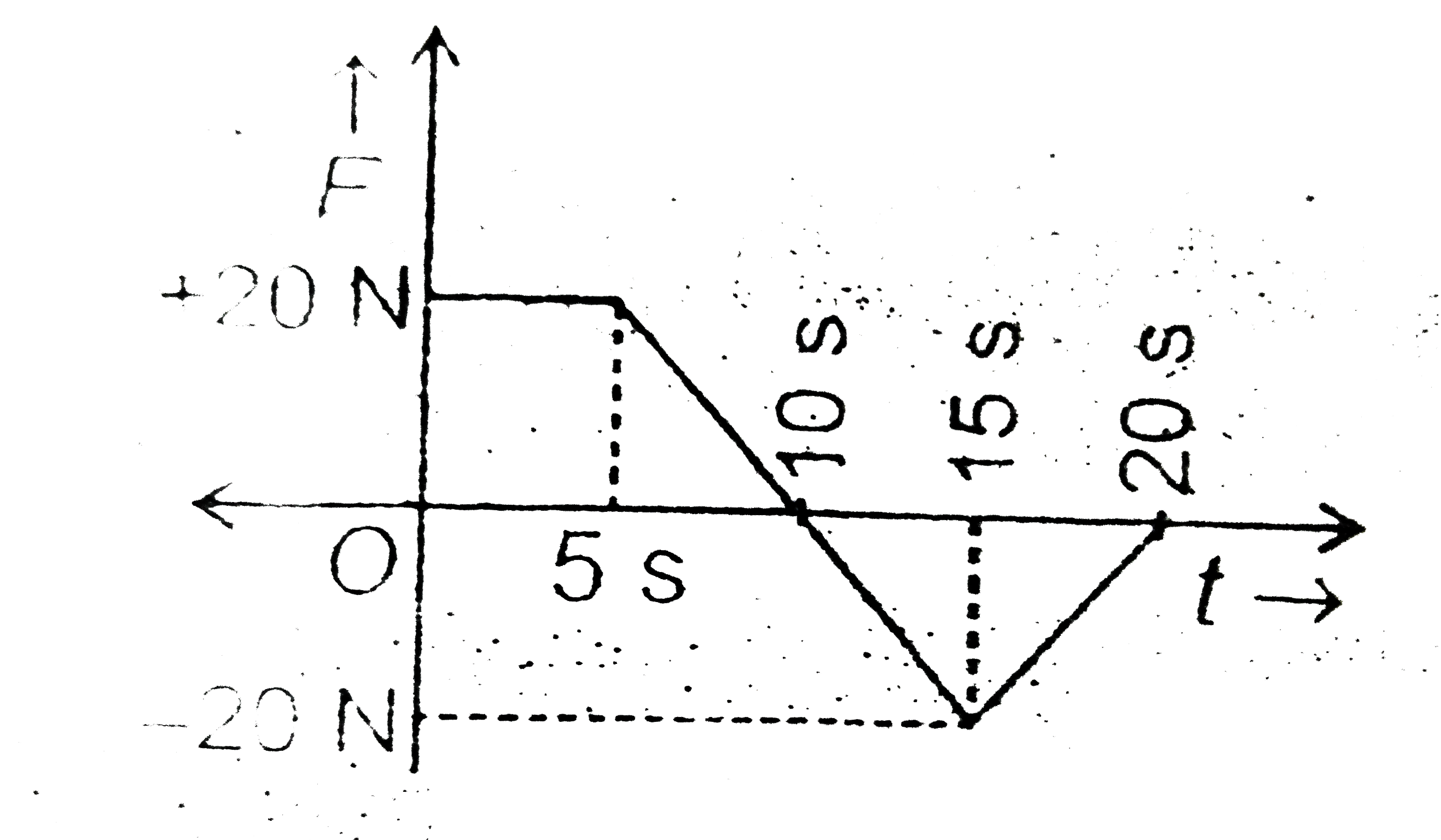
View SolutionA force vec(F)=2hat(i)-3hat(j)+7hat(k) (N) acts on a particle which undergoes a displacement vec(r )=7hat(j)+3hat(j)-2hat(k)(m) . Calculate the work done by the force.
View SolutionIf the work done on an object is 10 J and the object is displaced through 2 m, then what is the force applied?
View Solution