The electric curren in a charging R-C circuit is given by i=i0e−tRC when i0, R and C aere constant parameters of the circuit and t is time. Find the rate of change of current at a.t=0,b.t=RCc.t=10RC.Solution in Gujrati
The correct Answer is:(a)-i/RC (b)-i/Rce (c)-i/Rcxe^10
Given that, i=i0e−tRC,Rateofchan≥ofcurrent<br>=didt=i0(−1RC)e−tRC<br>=−i0RC×e−tRC<br>whena.t=0<br>didt=−i0Rcxe0=−i0RC<br>b.t=RC,didt=−i0Rcxe−1=−i0Rce<br>c.t=10,didt=−i0Rcxe10
Similar Questions
The electric current in a discharging R-C circuit is given by i=i0e−tRC where i0 Rand Care constant parameters and tis time. Let i0=2.00A, R=6.00×105ohm and C=0.500μF.
a. Find the current at t=0.3 s.
b. Find the rate of change of current at t=0.3 s.
Find approximately the current at t=0.31 s.
View SolutionThe current in a discharging LR circuit is given by I=i0(tτ) where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe current (i) at time t= 0 and t = oo respectively for the given circuit is :
View SolutionR-C Circuit at Time 't'
View SolutionA capacitor C and inductor L are connected in parallel with a battery of emf e and internal resistance r. At time t=0, current through the cell be i_0 and at t=0, current through the cellbe i_0 and at t rarroo let the current be i. then i_0/i is equal to
View SolutionThe current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionAn emf e=e0sinωt applied to a series L-C-R circuit derives a current I=I0sinωt in the circuit. Deduce the expression for the average power dissipated in the circuit.
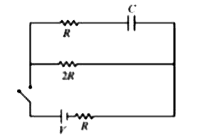
View SolutionIn the following RC circuit, key is kept closed for a long time and then it is opened at t=0. What is the current in resistance 2R after time t=3RC2?
View Solution