Check the dimensional of the wave y = sin(x-vt). If it is dimensionally wrong, write the above equation in the correct form.

Text Solution

Verified by Experts

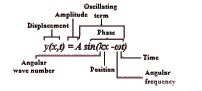
Dimensionally it is not correct. we know that y = sin(x-vt) must be a dimensionless quantity but x-vt has dimension. The correct equation is y= sin (k x- $ω$ t), where k and $ω$ have the dimensions of inverse of length and inverse of time respectively. The sine functions and cosine functions are periodic functions with period $2 π$ . Therefore, the correct expression is $y = sin (\frac{2 π}{λ} x - \frac{2 π}{T} t)$ where $λ$ and T are wavelength and time period, respectively. In general, $y (x, t) = A sin (k x - ω t)$
.

From the dimensional consideration, which of the following equations is correct?
A $T = 2 π \frac{\sqrt{R^{3}}}{G M}$
B $T = 2 π \frac{\sqrt{G M}}{R^{3}}$
C $T = 2 π \frac{\sqrt{G M}}{R^{2}}$
D $T = 2 π \sqrt{\frac{R^{2}}{G M}}$
From the dimensional consideration which of the following equation is correct ?
A $T = 2 π \sqrt{\frac{R^{3}}{G M}}$
B $T = 2 π \sqrt{\frac{G M}{R^{3}}}$
C $T = 2 π \sqrt{\frac{G M}{R^{2}}}$
D $T = 2 π \sqrt{\frac{R^{2}}{G M}}$
Which of the following equations is dimensionally correct?
Apressure = Engery per units volume
Bpressure = Energy per units area
Cpressure = Momentum $\times$ Volume $\times$ time
Dpressure = Force $\times$ area