There are eight persons A, B, C, D, E, F, G and H who were born on the same day of the same month of different year tile. 1950, 1954, 1962, 1971, 1978, 1982, 1995 and 1999 but not necessarily in the same order.
Note: Calculation done with respect to present year 2017 assuming month and date to be same as that of year of birth as next above. Each person is assumed to be born on same date & month of respected years.
F was born after 1978 but not born in 1995. Sum of present age of F and A is 81yr. Difference of present ages of A and H is less than nine. E is the oldest person. B was born in odd number year after H, but not born in 1995. Sum of present age of D and G is 61yr. D is younger than G.
Who is the fifth oldest person?
A
H
None of these
G
The correct Answer is:D
Step 1. From the given conditions, E is the oldest person. F was born after 1978 but not born in 1995. Sum of present age of F and A is 81yr. So, there will be two possible cases case 1 and case 2 in which F is either born, in 1982(then A is born in the year 1971) or in 1999(then A is born in the year 1954).

Step 2. As it is given that, Difference of present ages of A and His less than nine. B was born in odd number year after H, but not born in 1995.
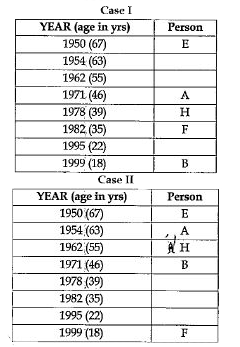
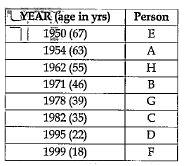
Step 3. Using the rest of the conditions, Sum of present age of D and G is 61yr. D is younger than G. So, from (these statement cases I will be eliminated. Now continuing with case II, G was born in the year 1978 and D in the year 1995 and C was born in the year 1982. Hence, we get our final solution.
Similar Questions
किसी ऐसे वर्ष में जो लीप वर्ष न हो 53 रविवार होने की प्रायिकता क्या है ?
View Solutionपांच तत्व A, B, C, D व E के E∘ क्रमशः −1.36,+0.32,+1.36,−0.42 तथा −2.2.6 है उनको बढ़ती सक्रियता के क्रम में लिखो ।
View Solutionसमान चालकता सेल में लिए गए दो विलयनों A तथा B के प्रतिरोध क्रमशः 50 ओम तथा 100 ओम है । यदि A व B के सामान आयतन मिला दिए जाये तो सामान चालकता सेल में मिश्रण का प्रतिरोध क्या होगा ?
(मोल A व B को मिलाने पर वियोजन की मात्रा में कोई परिवर्तन नहीं होता है)
View Solution18∘C व अनत तनुता पर H+ तथा CH3COO− की तुल्यांक चालकताएँ क्रमशः 315 तथा 35 महो सेमी2 तुल्यांक−1 है समान ताप पर ऐसीटिक अम्ल के 0.001 N विलयन की विशिष्ट चालकत्व 4.1×10−5महो सेमी−1 है ऐसीटिक अम्ल के वियोजन की मात्रा क्या होगी ?
View Solutionनीचे कुछ अभिक्रियाएँ दी गयी है-
(a) ACl2+B→BCl2+A
(b) B+DCl→ कोई अभिक्रिया नहीं
(c) C+2DCl→2D+CCl2
(d) C+ECl2→ कोई अभिक्रिया नहीं
(e) H2+ECl2→2HCl+E
(f) H2+FCl2→ कोई अभिक्रिया नहीं
उपरोक्त दिए तत्वों (A से F) को रासायनिक सक्रियता के घटते क्रम में व्यवस्थित करो ।
View Solutionएक ही ग्राफ पेपर पर x=0 और x=π2 के बीच sin x तथा cos x के लेखाचित्र खींचे तथा बताये की x के किस मान के लिए sin x = cos x होगा
View Solutionसंपारसरि विलयन का ………….. समान होता है .
View SolutionK4[Fe(CN)6] और Al2(SO4)3 में दोनों परासरण दाब एक समान होता है.
View Solution
