Total surface area of a cylinder mounted with a hemispherical bowl on one end is 2552 cm2. If height of cylinder is 8 cm then find the volume of the solid body?(cm3)
1044313
1067713
1054713
1097713
The correct Answer is:B
To solve the problem step by step, we need to find the volume of a solid body that consists of a cylinder with a hemispherical bowl on one end, given the total surface area and the height of the cylinder.
Step 1: Understand the given information
- Total Surface Area (TSA) of the solid = 2552 cm²
- Height of the cylinder (h) = 8 cm
- We need to find the radius (r) of the cylinder and the hemispherical bowl.
Step 2: Write the formula for the Total Surface Area
The total surface area of the cylinder with a hemispherical bowl on one end is given by:
TSA=2πr2+2πrh+πr2
Where:
- 2πr2 is the curved surface area of the cylinder,
- 2πrh is the lateral surface area of the cylinder,
- πr2 is the area of the base of the hemisphere.
Combining the terms, we have:
TSA=3πr2+2πrh
Step 3: Substitute the known values into the TSA equation
Substituting the known values into the TSA equation:
3πr2+2πr(8)=2552
This simplifies to:
3πr2+16πr=2552
Step 4: Factor out π
Dividing the entire equation by π (using π≈22/7 or 3.14):
3r2+16r=2552π
Using π≈22/7:
2552×722=812
So we have:
3r2+16r−812=0
Step 5: Solve the quadratic equation
Now we can use the quadratic formula r=−b±√b2−4ac2a where a=3, b=16, and c=−812:
b2−4ac=162−4×3×(−812)
Calculating:
=256+97224=97480
Now applying the quadratic formula:
r=−16±√974806
Calculating √97480≈312.2:
r=−16±312.26
Calculating the two possible values for r:
1. r=296.26≈49.37 (valid)
2. r=−328.26 (not valid as radius cannot be negative)
Step 6: Calculate the volume of the solid
The volume V of the solid body is given by the sum of the volume of the cylinder and the volume of the hemisphere:
V=Volume of Cylinder+Volume of Hemisphere
V=πr2h+23πr3
Substituting r=14 and h=8:
V=π(142)(8)+23π(143)
Calculating:
=π(196)(8)+23π(2744)
=1568π+54883π
=4704+54883π=101923π
Final Volume Calculation
Using π≈3.14:
V≈101923×3.14≈10677.33 cm3
Conclusion
The volume of the solid body is approximately 10677.33 cm3.
- Total Surface Area (TSA) of the solid = 2552 cm²
- Height of the cylinder (h) = 8 cm
- We need to find the radius (r) of the cylinder and the hemispherical bowl.
The total surface area of the cylinder with a hemispherical bowl on one end is given by:
TSA=2πr2+2πrh+πr2
Where:
- 2πr2 is the curved surface area of the cylinder,
- 2πrh is the lateral surface area of the cylinder,
- πr2 is the area of the base of the hemisphere.
TSA=3πr2+2πrh
Substituting the known values into the TSA equation:
3πr2+2πr(8)=2552
This simplifies to:
3πr2+16πr=2552
Dividing the entire equation by π (using π≈22/7 or 3.14):
3r2+16r=2552π
Using π≈22/7:
2552×722=812
So we have:
3r2+16r−812=0
Now we can use the quadratic formula r=−b±√b2−4ac2a where a=3, b=16, and c=−812:
b2−4ac=162−4×3×(−812)
Calculating:
=256+97224=97480
Now applying the quadratic formula:
r=−16±√974806
Calculating √97480≈312.2:
r=−16±312.26
Calculating the two possible values for r:
1. r=296.26≈49.37 (valid)
2. r=−328.26 (not valid as radius cannot be negative)
The volume V of the solid body is given by the sum of the volume of the cylinder and the volume of the hemisphere:
V=Volume of Cylinder+Volume of Hemisphere
V=πr2h+23πr3
Substituting r=14 and h=8:
V=π(142)(8)+23π(143)
Calculating:
=π(196)(8)+23π(2744)
=1568π+54883π
=4704+54883π=101923π
Using π≈3.14:
V≈101923×3.14≈10677.33 cm3
The volume of the solid body is approximately 10677.33 cm3.
Topper's Solved these Questions
- MENSURATION BOOK - ADDA247CHAPTER - MENSURATION EXERCISE - MAINS QUESTIONS
20 Videos
- MENSURATION BOOK - ADDA247CHAPTER - MENSURATION EXERCISE - PREVIOUS YEAR QUESTION
31 Videos
- MENSURATION BOOK - ADDA247CHAPTER - MENSURATION EXERCISE - PRELIMS QUESTIONS (LEVEL -1)
50 Videos
- INEQUALITYBOOK - ADDA247CHAPTER - INEQUALITYEXERCISE - Previous Year Questions
75 Videos
- MIXTURE & ALLIGATIONBOOK - ADDA247CHAPTER - MIXTURE & ALLIGATIONEXERCISE - PREVIOUS YEAR QUESTIONS
21 Videos
Similar Questions
Knowledge Check
The sum of the radius of the base of a solid cylinder and the height of the cylinder is 15 cm . If the total surface area of the cylinder is 660cm2 , then find the volume of the cylinder .
A1232cm3B1256cm3C1296cm3D1276cm3The area of base of a cylinder is 25πcm2. If the height of cylinder is 9cm, then find the total surface area of cylinder.
A440 cm2B240 cm2C420 cm2D220cm2
Find the total surface area of a hemispherical bowl of radius 5cm
View SolutionA solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
View SolutionThe total surface area of a cylinder of radius 7cm is 880cm2.
Find the height and the volume of the cylinder
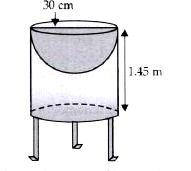
View SolutionMayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depr ession at one end . The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of bird bath.
View SolutionA solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid (Use π=22/7 )
View SolutionThe total surface area of a cylinder is 220cm2 and its height is 6.5 cm. Find its volume.
View Solution
