Initially one mole of ideal gas (Cv=52R) at 0.1 atm and 300 K is put through the following cycle:
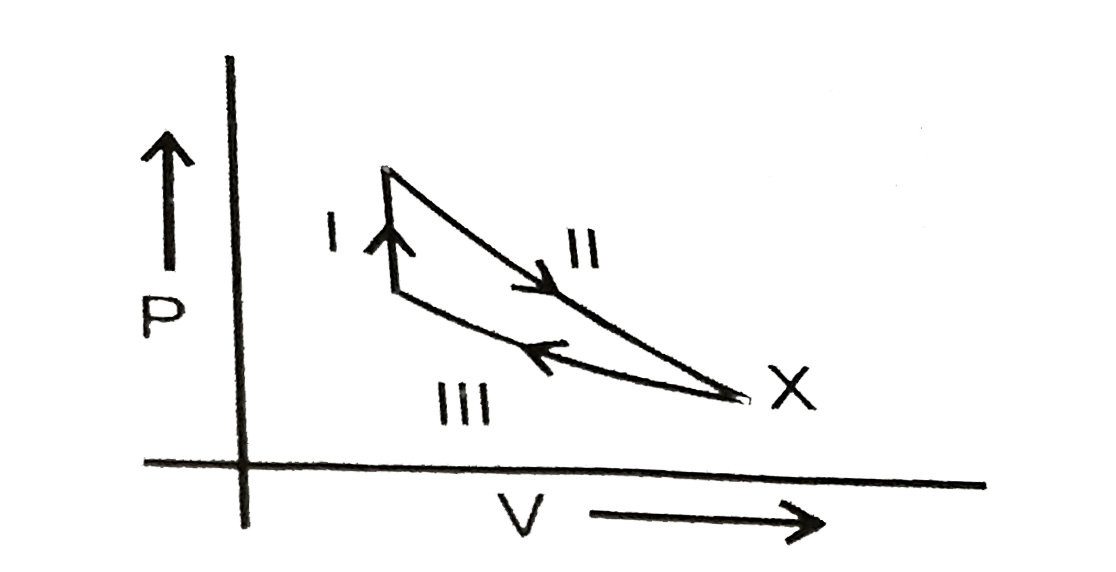
Step-I : Heating to twice its initial pressure at constant volume.
Step-II : Adiabatic expansion to its initial temperature.
Step-III : Isothermal compression back to 1.00 atm.
what is the volume at state X?Solution in Telugu
40.4 L
65.0 L
139 L
4.35 L
The correct Answer is:C
V1=24.63L T1=300K,T2=600K
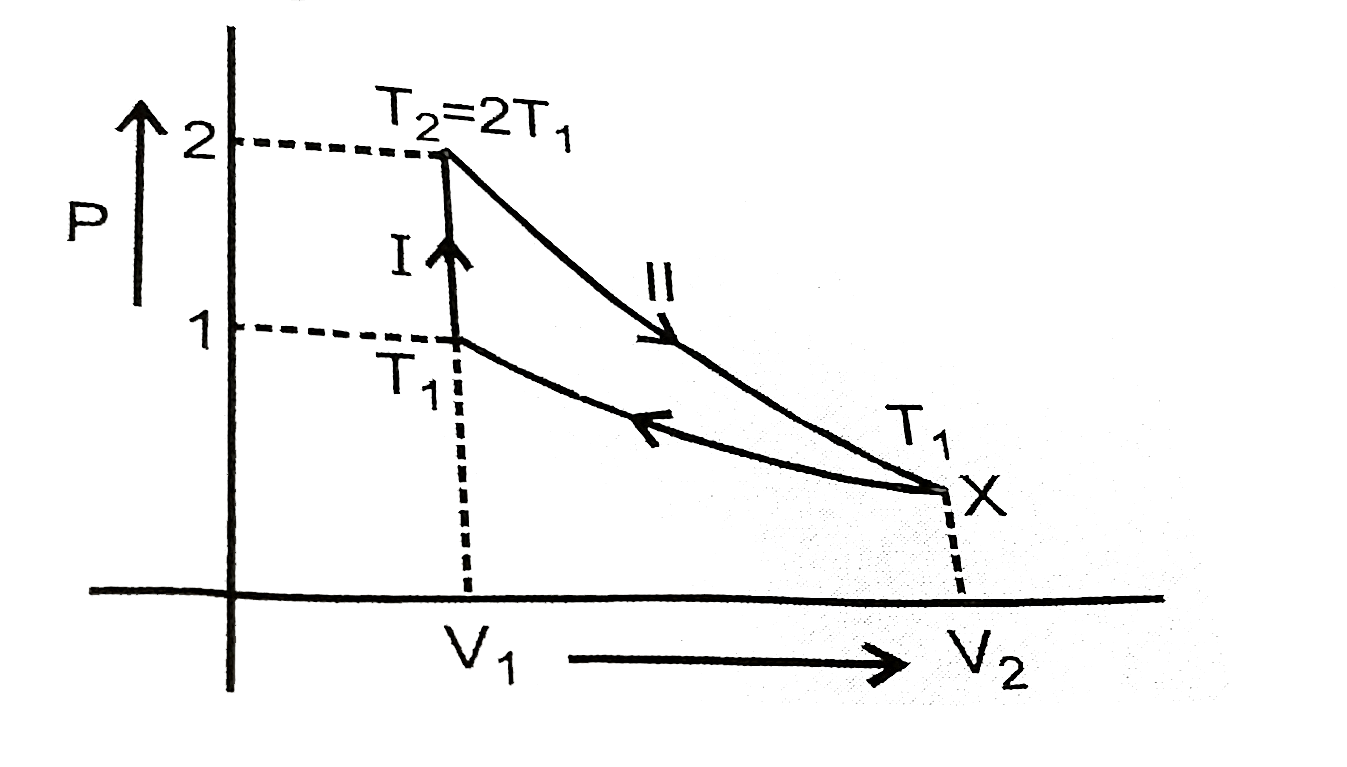
For path (II)
T1Vγ−11=T2Vγ−12
T1T2=(V2V1)γ−1
600300=(V2V1)75−1
(2)5/2=V2V1
V2=4√2×24.63=139.3L≈139L
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 1 (Q.1 To Q.30)
6 Videos
- THERMODYNAMICSBOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 1 (Q.31 To Q.60)
2 Videos
- STOICHIOMETRYBOOK - NARENDRA AWASTHICHAPTER - STOICHIOMETRYEXERCISE - Level 3 - Subjective Problems
20 Videos
Similar Questions
A system undergoes a process in which ΔU=+300J while absorbing 400 J of heat energy and undergoing an expansion against 0.5 bar. What is the change in the volume (in L)?
View SolutionA gas expands against a variable pressure given by P=20V (where P in atm and V in L). During expansion from volume of 1 litre to 10 litre, the gas undergoes a change in internal energy of 400 J. How much heat is absorbed by the gas during expansion?
View SolutionWhat volume of a liquid (in L) will contain 10 mole ? If molar mass of liquid is 280 and its density is 1.4 g/mL.
View SolutionAn ideal gas undergoes isothermal expansion followed by heat removel at constant volume and they by heat removal at constant pressure to the initial volume. The correct descripion of these steps is indicated by
View SolutionOne mole of an ideal gas (C_(v,m)=(5)/(2)R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas :
View SolutionWhen one mole of an ideal gas is compressed to half of its initial volume and simultaneously heated to twice its initial temperature, the change in entropy of gas (DelataS) is:
View SolutionOne mole of an ideal gas (C_(v,m)=(5)/(2)R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas is :
View SolutionInitially one mole of ideal gas (Cv=52R) at 0.1 atm and 300 K is put through the following cycle:

Step-I : Heating to twice its initial pressure at constant volume.
Step-II : Adiabatic expansion to its initial temperature.
Step-III : Isothermal compression back to 1.00 atm.
what is the volume at state X?
View SolutionTwo moles of an ideal gas (CV=52R) was compressed adiabatically against constant pressure of 2 atm .
Which was initially at 350 K and 1 atm pressure. The work involve in the process is equal to.
View SolutionWhen one mole of an ideal gas is compressed to half of its initial volume and simultaneously heated to twice its initial temperature , the change in entropy of gas (DeltaS) is :
View SolutionSuppose 1.00 L of a gas with γ= 1.30, initially at 285 K and 1.00 atm, is suddenly compressed adiabatically to half its initial volume. Find its final (a) pressure and (b) temperature. (C) If the gas is then cooled to 273 K at constant pressure, what is its final volume?
View SolutionAt a constant temperature a gas is initially at 2 atm pressure. To compress it to 1/8th of its initial volume, pressure to be applied is
View SolutionOne mole of an ideal gas (C_(v,m)=(5)/(2)R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas is :
View SolutionWhen one mole of an ideal gas is compressed to half of its initial volume and simultaneously heated to twice its initial temperature, the change in entropy of gas (DelataS) is:
View SolutionInitially one mole of ideal gas (Cv=52R) at 0.1 atm and 300 K is put through the following cycle:

Step-I : Heating to twice its initial pressure at constant volume.
Step-II : Adiabatic expansion to its initial temperature.
Step-III : Isothermal compression back to 1.00 atm.
what is the volume at state X?
View SolutionAn ideal gas undergoes isothermal expansion followed by heat removel at constant volume and they by heat removal at constant pressure to the initial volume. The correct descripion of these steps is indicated by
View Solution
