The efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be
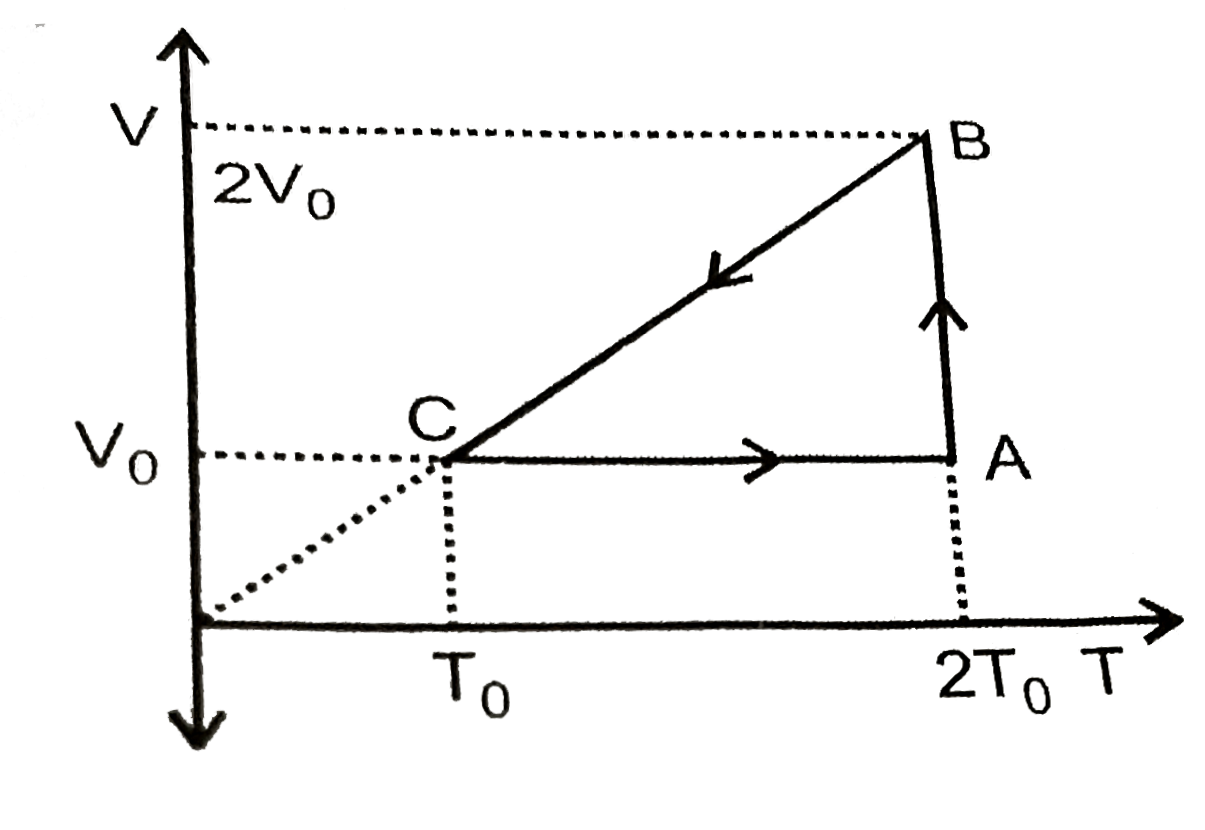 Solution in Telugu
Solution in Telugu
(γ−1)(2 ln 2−1)1+(γ−1)2 ln 2
(γ−1)(1−2 ln 2)(γ−1)2 ln 2−1
(2 ln 2+1)(γ−1)(γ−1)2 ln 2+1
(2 ln 2−1)γ/(γ−1)
The correct Answer is:A
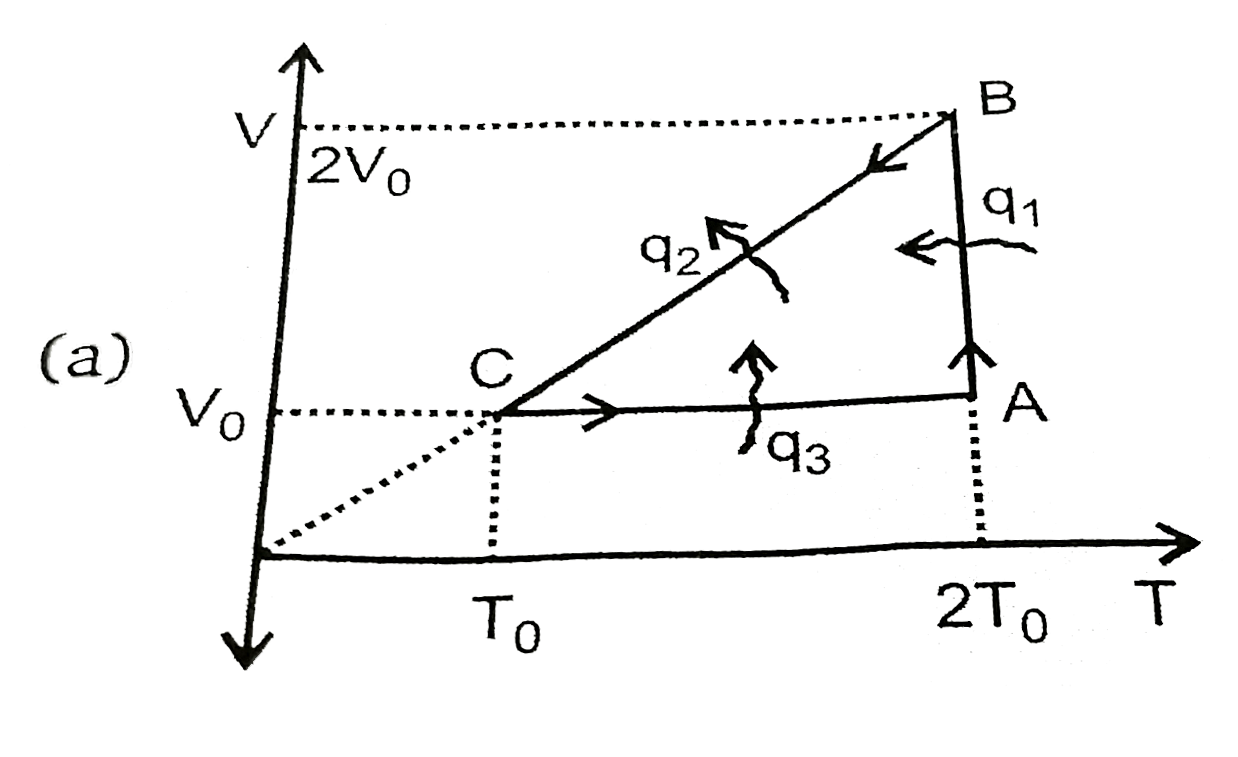
AB process
0=q1+w1
=q1−nR(2T0)ln2
BC process ΔU2=q2+w2
nR(γ−1)(T0−2T0)=q2−(nRT0V0).(V0−2V0)
CA process
ΔU3=q3+w3
nR(γ−1)(2T0−T0)=q3+0
Efficiency =Total work doneTotal heat absorbed=w1+w2q1+q3
=(−2RT0ln2)+(nRT0)(2RT0ln2)+(nRT0γ−1)
Topper's Solved these Questions
- THERMODYNAMICSBook:NARENDRA AWASTHIChapter:THERMODYNAMICSExercise:Level 1 (Q.1 To Q.30)
Explore 6 Videos
- THERMODYNAMICSBook:NARENDRA AWASTHIChapter:THERMODYNAMICSExercise:Level 1 (Q.31 To Q.60)
Explore 2 Videos
- STOICHIOMETRYBook:NARENDRA AWASTHIChapter:STOICHIOMETRYExercise:Level 3 - Subjective Problems
Explore 20 Videos
Similar Questions
A system undergoes a process in which ΔU=+300J while absorbing 400 J of heat energy and undergoing an expansion against 0.5 bar. What is the change in the volume (in L)?
View SolutionA gas expands against a variable pressure given by P=20V (where P in atm and V in L). During expansion from volume of 1 litre to 10 litre, the gas undergoes a change in internal energy of 400 J. How much heat is absorbed by the gas during expansion?
View SolutionWhat volume of a liquid (in L) will contain 10 mole ? If molar mass of liquid is 280 and its density is 1.4 g/mL.
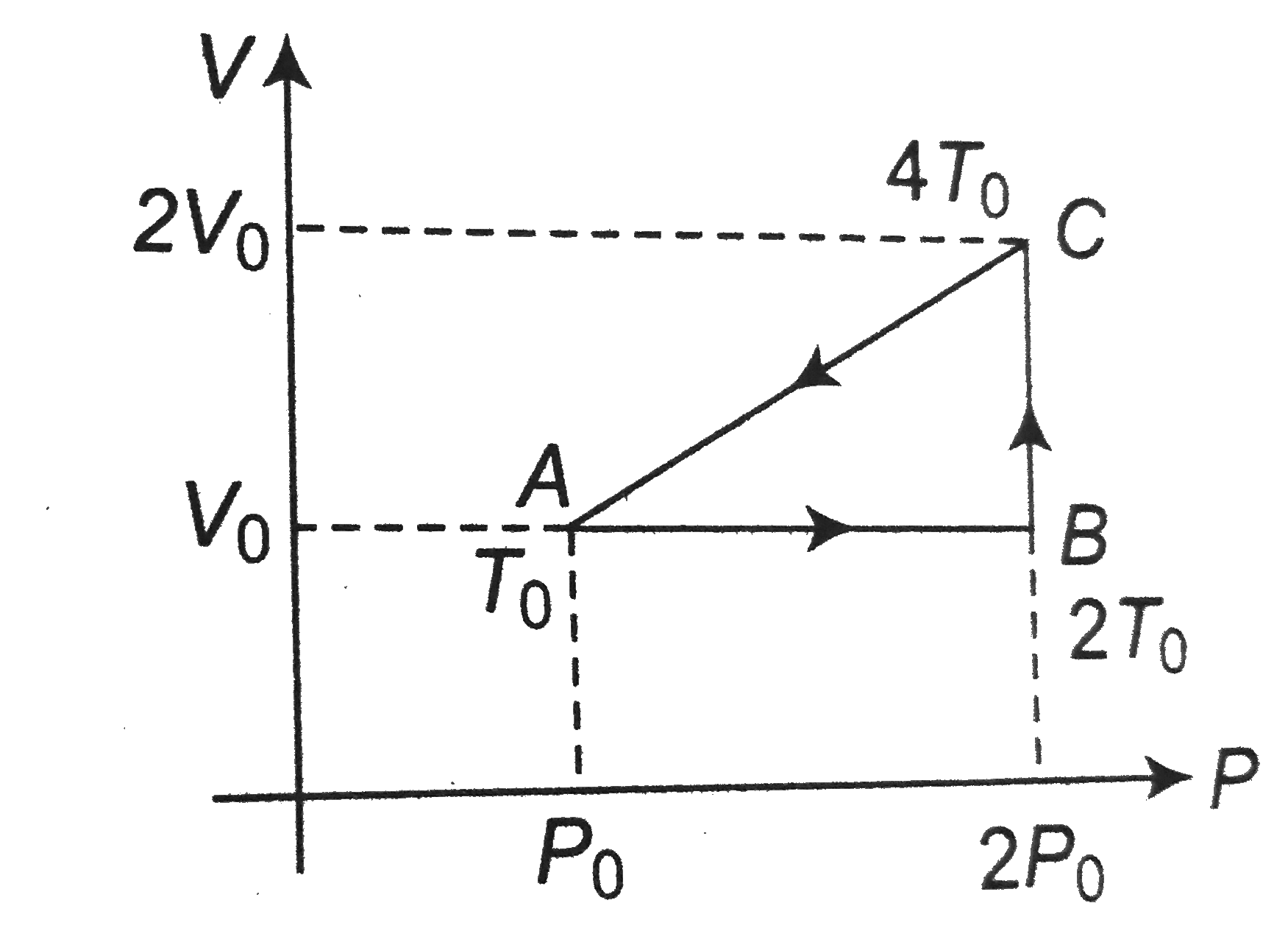
View SolutionA thermodynamic process of one mole ideal monoatomic gas is shown in figure. The efficiency of cyclic process ABCA will be
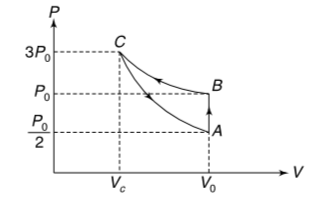
View SolutionOne mole of an ideal gas is carried through a thermodynamics cycle as shown in the figure. The cycle consists of an isochoric, an isothermal and an adiabatic process. Find the adiabatic exponent of the gas.
View SolutionThe efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be

View SolutionA gas of adiabatic exponent γ is supplied heat at a constant pressure. Show that in such a process ΔQ:ΔW=γ:1:(γ−1).
View SolutionThe relation between U, p and V for an ideal gas in an adiabatic process is given by relation U=a+bpV . Find the value of adiabatic exponent (gamma) of this gas.
View SolutionThe efficiency of an ideal gas with adiabatic exponent 'gamma' for the shown cyclic process would be
View SolutionTwo moles of an ideal gas goes under the process shown in figure. AB and CD are reversible adiabatic process. The efficiency of the cycle is
View SolutionAn ideal gas undergoes a cyclic process as shown in the given P-T diagram, where AC is adiabatic. The process is also represented by:
View SolutionA monoatomic ideal gas through a cyclic process as shown in the figure . The efficiency of this process is
View SolutionFind the molar heat capacity of an ideal gas with adiabatic exponent gamma for the polytorpic process PV^(n)= Constant.
View SolutionA thermodynamic process of one mole ideal monatomic gas 2.is shown in figure. The 4 efficiency of cyclic process ABCA will be
View SolutionThe efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be

View SolutionA thermodynamic process of one mole ideal monoatomic gas is shown in figure. The efficiency of cyclic process ABCA will be
View Solution