The molar entropies of HI(g),H(g)andI(g) at 298K are 206.5, 114.6, and 180.7Jmol−1K−1 respectively. Using the ΔG∘ given below, calculate the bond energy of HI.
HI(g)→H(g)+I(g),ΔG∘=271.8kJ (Give your answer after divide with 49.7)Solution in Telugu
282.4kJmol−1
298.3kJmol−1
290.1kJmol−1
315.4kJmol−1
The correct Answer is:B
ΔS∘=−206.5+114.6+180.7=88.8
ΔG∘=ΔH∘−TΔS∘
ΔH∘=271.8+298×88.8×10−3
ΔH∘=298.3
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 1 (Q.121 To Q.150)
1 Videos
- THERMODYNAMICSBOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 2 (Q.1 To Q.30)
1 Videos
- THERMODYNAMICSBOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 1 (Q.31 To Q.60)
2 Videos
- STOICHIOMETRYBOOK - NARENDRA AWASTHICHAPTER - STOICHIOMETRYEXERCISE - Level 3 - Subjective Problems
20 Videos
Similar Questions
Gasoline has an enthalpy of combustion 24000 kJ/mol gallon. When gasoline burns in an automobile engine, approximately 30% of the energy released is used to produce mechanical work. The remainder is lost as heat transfer to the engine's cooling system. As a start on estimating how much heat transfer is required, calculate what mass of water could be heated from 25∘C to 75∘C by the combustion of 1.0 gallon of gasoline in an automobile? (Given : C(H2O)=4.18J/g∘C)
View SolutionTwo moles of a triatomic linear gas (neglect vibration degree of freedom) are taken through a reversible process ideal starting from A as shown in figure.
The volume ratio VBVA=4. If the temperature at A is −73∘C, then :
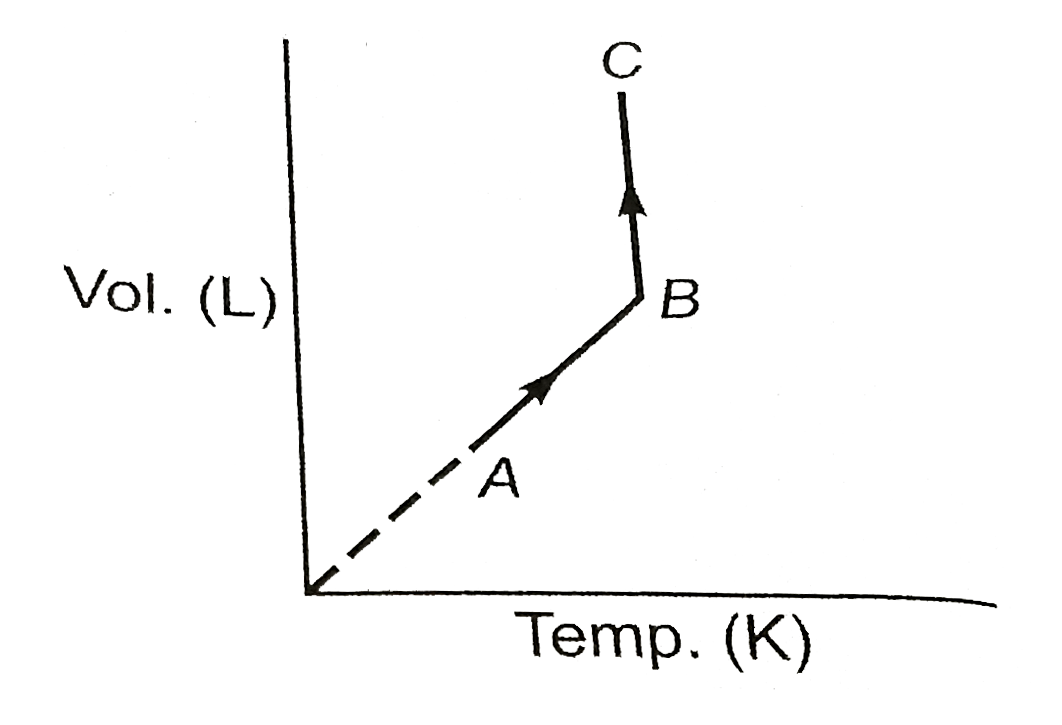
(ii) Total enthalpy change in both steps is :
View SolutionA gas expands against a variable pressure given by P=20V (where P in atm and V in L). During expansion from volume of 1 litre to 10 litre, the gas undergoes a change in internal energy of 400 J. How much heat is absorbed by the gas during expansion?
View SolutionWhat volume of a liquid (in L) will contain 10 mole ? If molar mass of liquid is 280 and its density is 1.4 g/mL.
View SolutionFor the reaction, 2NO_(g) + O_(2)(g) rarr 2NO_(2)(g) Calculate DeltaG at 700K when enthalpy and entropy changes are -113.0 kJ mol^(-1) and -145 J K^(-1) mol^(-1) , respectively.
View SolutionThe entropies of H_(2) (g) and H (g) are 130.6 and 114.6 J mol^(-1)K^(-1) respectively at 298 K. Using the data given below calculate the bond energy of H_(2) (in kJ/mol) : H_(2)(g)rarr2H(g),DeltaG^(@)=406.6kJ
View SolutionThe molar entropies of HI(g), H(g) and I(g) at 298 K are 206.5, 114.6, and 180.7 J mol^(-1)K^(-1) respectively. Using the DeltaG^(@) given below, calculate the bond energy of HI. HI(g)rarrH(g)+I(g)," "DeltaG^(@)=271.8 kJ
View SolutionThe entropies of H2(g) and H(g) are 130.6 and 114.6Jmol−1K−1 respectively at 298 K. Using the data given below calculate ΔH∘ ( in kJ/ mol) of the reaction given below.
H2(g)→2H(g) , ΔG∘=406.62kJ/mol
View SolutionThe entropies of H_(2)(g) and H(g) are 60 " and " 50 J"mole"^(-1)K^(-1) respectively at 300 K. Using the data given below calcualate the bond enthalpy of H_(2)(g) in Kcal "mole"^(-1) . " "H_(2)(g) rarr 2H(g)," "DeltaG^(@)=21.6 KJ "mole"^(-1)
View SolutionDeltaG^(@)(HI,g)-=+1.7kJ. What is the equilibrium constnt at 25^(@)C"for"2 HI_((g))hArrH_(2(g))+I_(2(g))
View Solutionयदि अभिक्रिया H2(g)+I2(g)⇔2HI(g) के लिए K का मान 48 ह तब अभिक्रिया 12H2(g)+12I2⇔HIg के लिए K का मान क्या होगा ?
View Solutionwill the reaction, I_(2_((g)))+H_(2)S_((g))rarr2HI_((g))+S_((s)) proceed spontaneously in the forward direction at 298K ? You are given with DeltaG^(@) for HI and H_(2) as 1.8 and -33.8 kJ mol^(-1) respectively . Given : I_(2_((g)))+H_(2)S_((g))rarr2HI_((g))+S_((s)) DeltaG_(HI)^(@)=1.8kJ mol^(-1) DeltaG_(H_(2)S)^(@)=1.8kJ mol^(-1)
View SolutionCalculate the standard free energy change (ΔG∘) of the following reaction and say whether it is feasible at 373 K or not 12H2(g)+12I2(g)→HI(g),ΔH∘ris + 25.95 kJ mole−1. Standard entropies of HI(g).H2(g)andI2(g) are 206.3, 130.6 and 116.7JK−1mole−1.
View SolutionThe molar entropies of HI(g),H(g)andI(g) at 298K are 206.5, 114.6, and 180.7Jmol−1K−1 respectively. Using the ΔG∘ given below, calculate the bond energy of HI.
HI(g)→H(g)+I(g),ΔG∘=271.8kJ (Give your answer after divide with 49.7)
View SolutionH_(2(g)) reacts with I_(2(g)) to give HI_((g)) . Write the rate equation and predict order.
View SolutionH2(g) reacts with I2(g) to give HI(g). Write the rate equation and predict order of the reaction with respect to H2 and I2.
View Solution
