In a stationary shop there are four types of colored sheets of red , blue ,green and white colors . The probability of selecting one red sheet out of the total sheets is , the probability of selecting one blue sheet out of the sheets is and the probability of selecting one white sheet out of the total sheets is .the number of green sheets in the bag is 22.
What is the total number of sheets in the bag ?
A)117
B)168
C)154
D)120
The correct Answer is:B
To find the total number of sheets in the bag, we can follow these steps:
Step 1: Define the Variables
Let the total number of sheets in the bag be T. We know the number of green sheets is 22.
Step 2: Write the Probabilities
We are given the probabilities of selecting each color sheet:
- Probability of selecting a red sheet: P(R)=13
- Probability of selecting a blue sheet: P(B)=27
- Probability of selecting a white sheet: P(W)=14
- Probability of selecting a green sheet: P(G)=22T
Step 3: Set Up the Equation
The sum of the probabilities of selecting each color sheet must equal 1:
P(R)+P(B)+P(W)+P(G)=1
Substituting the known probabilities:
13+27+14+22T=1
Step 4: Find a Common Denominator
To add the fractions, we need a common denominator. The least common multiple (LCM) of 3, 7, and 4 is 84. We convert each fraction:
- 13=2884
- 27=2484
- 14=2184
Step 5: Substitute Back into the Equation
Now substitute these values back into the equation:
2884+2484+2184+22T=1
Combine the fractions:
28+24+2184+22T=1
This simplifies to:
7384+22T=1
Step 6: Isolate the Fraction
Rearranging the equation gives:
22T=1−7384
Calculating the right side:
1−7384=84−7384=1184
Thus, we have:
22T=1184
Step 7: Cross-Multiply to Solve for T
Cross-multiplying gives:
22⋅84=11⋅T
Calculating 22⋅84:
1848=11T
Now, divide both sides by 11:
T=184811=168
Conclusion
The total number of sheets in the bag is T=168.
---
Let the total number of sheets in the bag be T. We know the number of green sheets is 22.
We are given the probabilities of selecting each color sheet:
- Probability of selecting a red sheet: P(R)=13
- Probability of selecting a blue sheet: P(B)=27
- Probability of selecting a white sheet: P(W)=14
- Probability of selecting a green sheet: P(G)=22T
The sum of the probabilities of selecting each color sheet must equal 1:
P(R)+P(B)+P(W)+P(G)=1
Substituting the known probabilities:
13+27+14+22T=1
To add the fractions, we need a common denominator. The least common multiple (LCM) of 3, 7, and 4 is 84. We convert each fraction:
- 13=2884
- 27=2484
- 14=2184
Now substitute these values back into the equation:
2884+2484+2184+22T=1
Combine the fractions:
28+24+2184+22T=1
This simplifies to:
7384+22T=1
Rearranging the equation gives:
22T=1−7384
Calculating the right side:
1−7384=84−7384=1184
Thus, we have:
22T=1184
Cross-multiplying gives:
22⋅84=11⋅T
Calculating 22⋅84:
1848=11T
Now, divide both sides by 11:
T=184811=168
The total number of sheets in the bag is T=168.
Topper's Solved these Questions
- PERMUTATION ,COMBINATION AND PROBABILITY Book:ADDA247Chapter:PERMUTATION ,COMBINATION AND PROBABILITY Exercise:Previous Year Question
Explore 25 Videos
- PERMUTATION ,COMBINATION AND PROBABILITY Book:ADDA247Chapter:PERMUTATION ,COMBINATION AND PROBABILITY Exercise:Prelims Questions (Level - 2)
Explore 35 Videos
- PERCENTAGEBook:ADDA247Chapter:PERCENTAGEExercise:PREVIOUS YEAR QUESTION
Explore 26 Videos
- PROFIT AND LOSSBook:ADDA247Chapter:PROFIT AND LOSSExercise:Previous Year Questions
Explore 30 Videos
Similar Questions
Knowledge Check
The cost of 312 metre sheet is Rs.150, what will be the cost of 1 metre sheet ?
AApprox. Rs. 43BRs. 43CRs. 44DApprox. Rs. 43.50Figure shows a thin metallic triangular sheet ABC. The mass of the sheet is M. The moment of inertia of the sheet about side AC is :
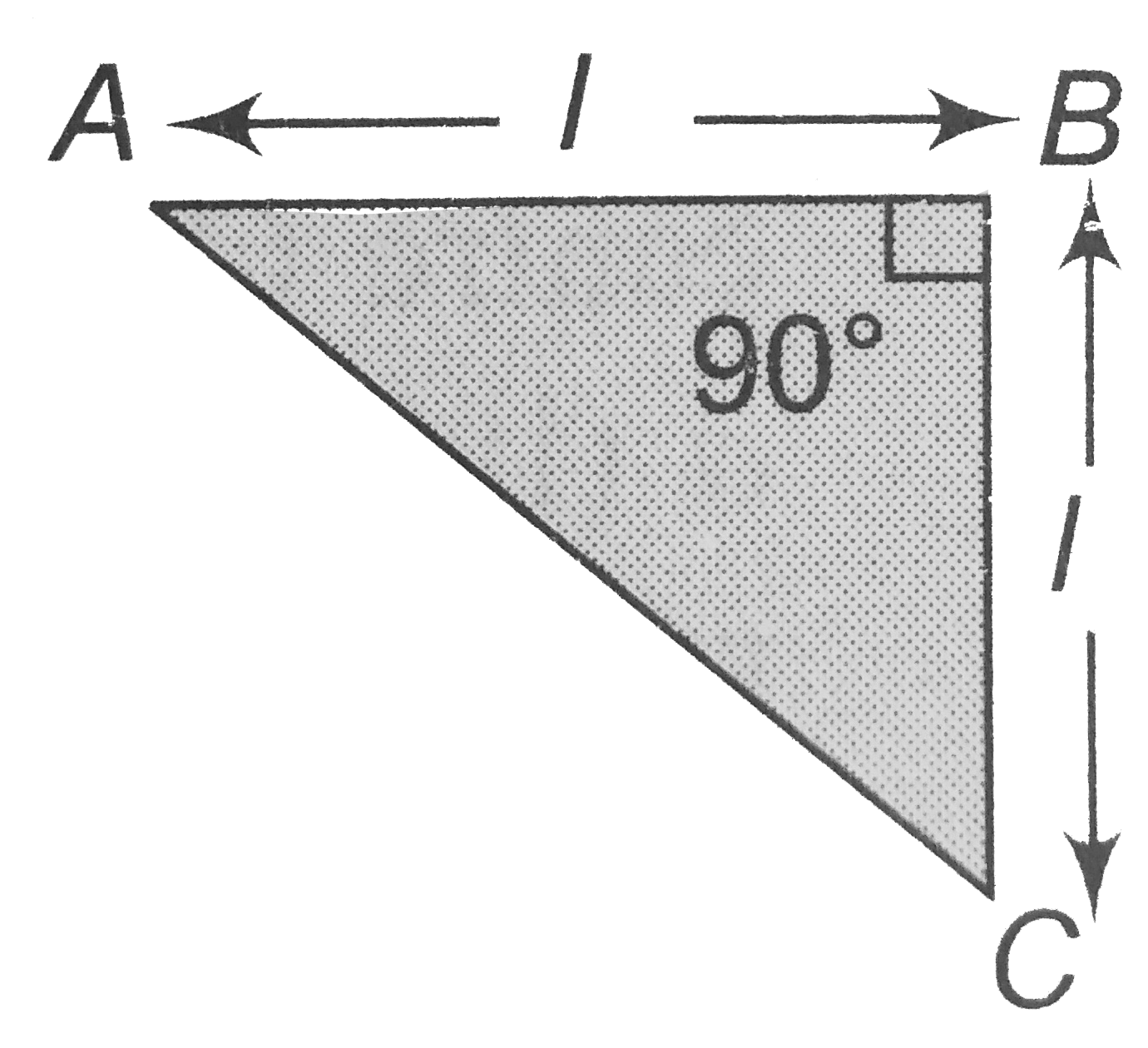 .AMl218BMl212CMl26DMl24
.AMl218BMl212CMl26DMl24Out of the four alternatives, choose the one which best expresses the meaning of the given and mark it in the Answer sheet.
TARDYALateBQuickCPromptDGradual
The area of a square sheet is 250 sq. cm. If one-fourth of the sheet is painted red, then half of the sheet is painted green and the remaining is painted white. Find the percentage of the area painted in white.
View SolutionDefects on plywood sheet occur at random with the average of one defect per 50 Sq. ft. Find the probability that such a sheet has no defect. Use e−1=0.3678.
View SolutionOut of the four alternatives, choose the one which best expresses the meaning of the given and mark it in the Answer sheet.
PROUD
View SolutionOut of the four alternatives, choose the one which best expresses the meaning of the given and mark it in the Answer sheet.
VAGUE
View SolutionOut of the four alternatives, choose the one which best expresses the meaning of the given and mark it in the Answer sheet.
SMUG
View Solution