Question

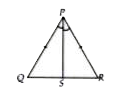
PQR is an isosceles triangle with such that $PQ=PR=15$ cm and $QR=24$cm. PS is a perpendicular bisector of the base QR. What is the length (in cm) of PS?

Options

A. 18
B. 6
C. 12
D. 9

Answer

D

Explanation

To find the length of PS in the isosceles triangle PQR, we can follow these steps:

Step 1: Understand the Triangle
We have an isosceles triangle PQR where:
- PQ = PR = 15 cm (the equal sides)
- QR = 24 cm (the base)

Step 2: Find the Midpoint of QR
Since PS is the perpendicular bisector of QR, we first need to find the midpoint S of QR. The length of QR is 24 cm, so:
- QS = SR = QR/2 = 24 cm / 2 = 12 cm.

Step 3: Apply the Pythagorean Theorem
In triangle PQS (which is a right triangle), we can apply the Pythagorean theorem:
- PQ² = PS² + QS²

We know:
- PQ = 15 cm
- QS = 12 cm

Step 4: Substitute the Values into the Equation
Now we substitute the known values into the equation:
- 15² = PS² + 12²

Calculating the squares:
- 225 = PS² + 144

Step 5: Solve for PS²
Now we can isolate PS²:
- PS² = 225 - 144
- PS² = 81

Step 6: Find PS
Now, take the square root of both sides to find PS:
- PS = √81
- PS = 9 cm

Final Answer
The length of PS is 9 cm.

---