What does 'K' represent in the equation given below?
dNdt=rN(K−NK)
1)Population density at time 't'
2)Intrinsic rate of natural increase
3)Carrying capacity
4)The base of natural logarithm
The correct Answer is:C
To solve the question, we need to analyze the equation provided and identify what 'K' represents in the context of the logistic population growth model.
1. Understand the Equation: The equation given is dNdt=rN(K−NK). This is a differential equation that describes how a population changes over time.
2. Identify the Variables:
- N: This represents the population density at time 't'.
- r: This is the intrinsic rate of natural increase of the population.
- K: This is the variable we need to identify.
3. Analyze the Role of K: In the context of the logistic growth model, 'K' is known as the carrying capacity. The carrying capacity is the maximum population size that an environment can sustain indefinitely without being degraded.
4. Eliminate Incorrect Options:
- Option 1: Population density at time t is represented by 'N', not 'K'.
- Option 2: The intrinsic rate of natural increase is represented by 'r', not 'K'.
- Option 4: The base of the natural logarithm is 'e', not 'K'.
5. Conclusion: Since 'K' represents the carrying capacity in the logistic growth model, the correct answer is that 'K' represents the carrying capacity.
Final Answer:
K represents the carrying capacity.
---
- N: This represents the population density at time 't'.
- r: This is the intrinsic rate of natural increase of the population.
- K: This is the variable we need to identify.
- Option 1: Population density at time t is represented by 'N', not 'K'.
- Option 2: The intrinsic rate of natural increase is represented by 'r', not 'K'.
- Option 4: The base of the natural logarithm is 'e', not 'K'.
K represents the carrying capacity.
Topper's Solved these Questions
- ORGANISMS AND POPULATIONSBook:AAKASH SERIESChapter:ORGANISMS AND POPULATIONSExercise:EXERCISE-I (LIFE HISTORY VARIATION)
Explore 3 Videos
- ORGANISMS AND POPULATIONSBook:AAKASH SERIESChapter:ORGANISMS AND POPULATIONSExercise:EXERCISE-I (POPULATION INTERACTIONS)
Explore 46 Videos
- ORGANISMS AND POPULATIONSBook:AAKASH SERIESChapter:ORGANISMS AND POPULATIONSExercise:EXERCISE-I (ADAPTATIONS)
Explore 12 Videos
- NEURAL CONTROL AND COORDINATIONBook:AAKASH SERIESChapter:NEURAL CONTROL AND COORDINATIONExercise:EXERCISE-III( PREVIOUS AIPMT / NEET QUESTIONS)
Explore 33 Videos
- PHOTOSYNTHESIS IN HIGHER PLANTS Book:AAKASH SERIESChapter:PHOTOSYNTHESIS IN HIGHER PLANTS Exercise:Exercise - III
Explore 27 Videos
Similar Questions
Knowledge Check
The population growth is generally described by the following equation : dNdt=rN(K−NK) What does 'r' represent in the given equation ?
APopulation density at time 't'BIntrinsic rate of natural increaseCCarrying capacityDThe base of natural logarithm
What is 'r' in the population equation given : dN/dt = rN
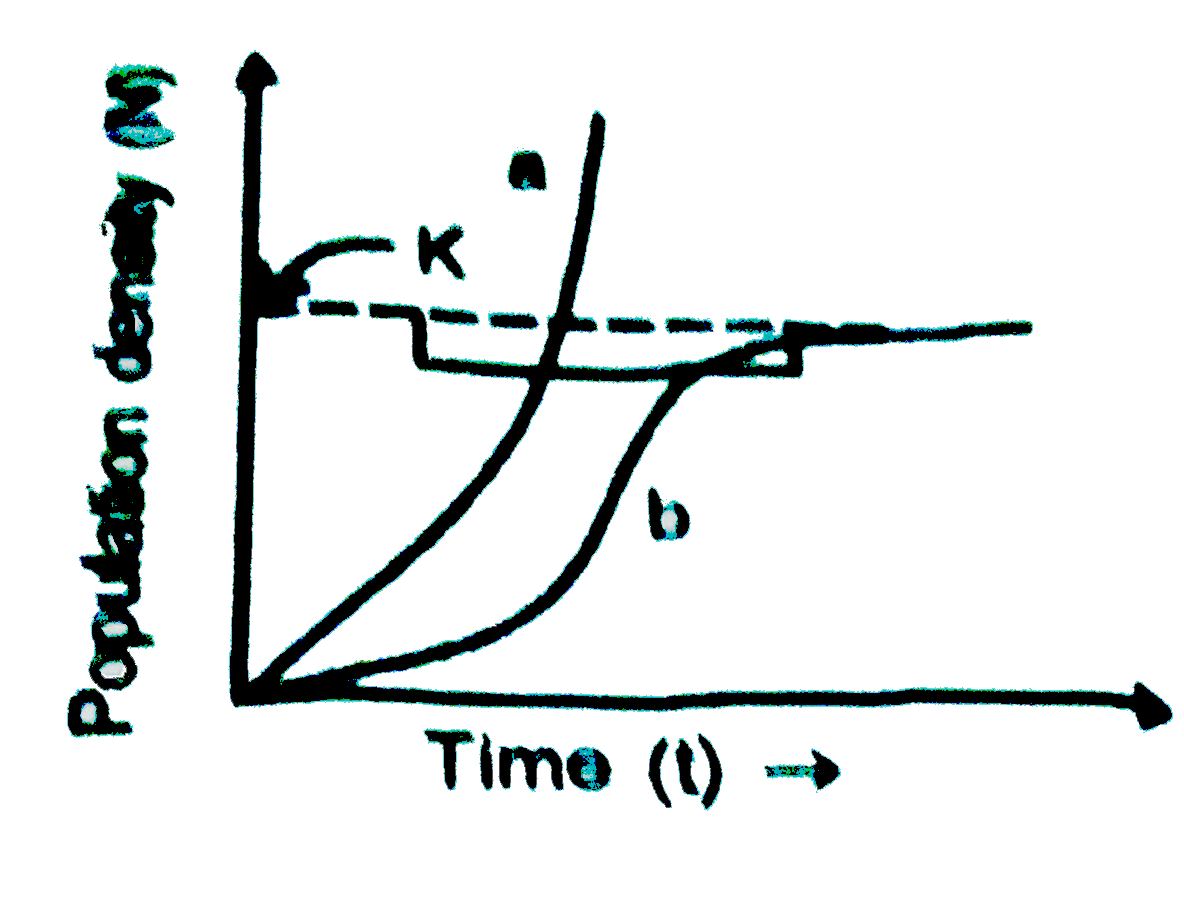
View SolutionStudy the graph given below and answer the questions that follow :
(i) The curve 'b' is described by the following equation :
dNdt=rN{K−NK}
(ii) What does 'K' stand for in this equation ? Mention its significance.
(ii) Which one of the two curves is considered a more realistic one for most of the animal populations ?
(iii) Which curve would depict the population of a species of deer if there are no predators in the habitat ? Why is to so ?
View SolutionIn the equation,dN/dt=rN
View SolutionStudy the population growth curves in the graph given below and answer the questions which follow :
(i) Identify the growth curves ‘a’ and ‘b’.
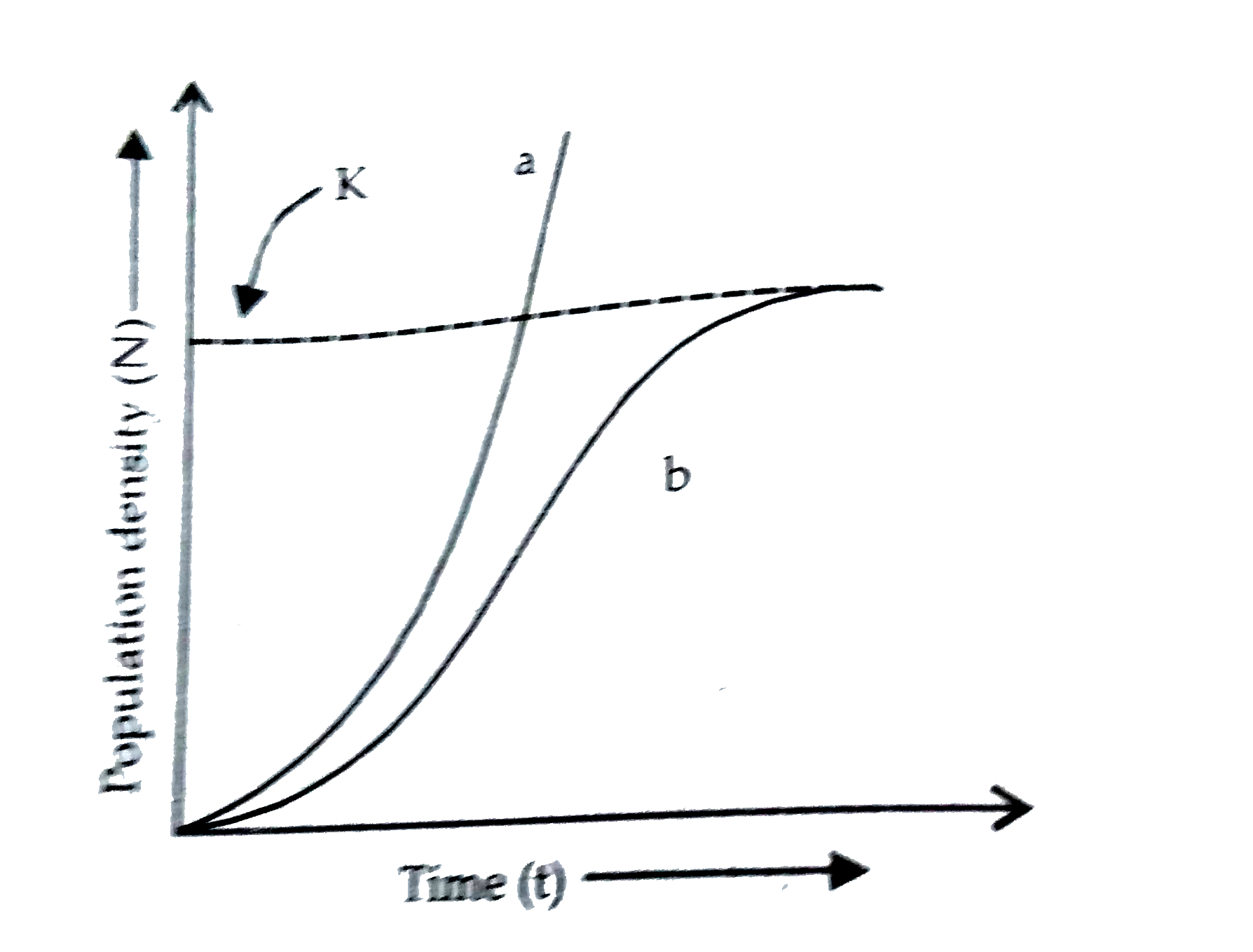
(ii) Which one. of them is considered a more realistic one and why ?
If dN9dt)=rN(K−NK) is the equation of the logistic growth curve, what does K stand for ?
(iv) What is symbolised by N ?
View SolutionCarrying capacity in equation dNdt=rN[K−Nk] is :
View Solutionwhich of the following option is true for verhulst Pearl logistic growth?
(A)population growth is decreased by the equation dNdt=rN[KK−N].
(B) r' represents biotic potential.
(C) applicable to a population growing in habitat with limited resources.
(D)K represents carrying capacity
View SolutionWhen does the growth rate of a population following the logistic model equal zero ? The logistic model is given as dN/dt = rN(1-N/K):
View Solution

