Two forces F, F have an angle α , between them , their resultant has magnitude of
The correct Answer is:2Fcosα2
To find the magnitude of the resultant of two forces F and F that have an angle α between them, we can use the law of cosines. Here’s a step-by-step solution:
Step 1: Identify the Forces and Angle
We have two forces:
- Force 1: F
- Force 2: F
- Angle between them: α
Step 2: Apply the Law of Cosines
The magnitude of the resultant R of two vectors can be calculated using the formula:
R=√F21+F22+2F1F2cos(α)
Step 3: Substitute the Values
Since both forces are equal in magnitude, we can substitute F1=F and F2=F:
R=√F2+F2+2F⋅Fcos(α)
Step 4: Simplify the Expression
Combine the terms:
R=√F2+F2+2F2cos(α)=√2F2+2F2cos(α)
Step 5: Factor Out Common Terms
Factor out 2F2:
R=√2F2(1+cos(α))
Step 6: Further Simplify
Taking the square root of the factored expression gives:
R=√2F√1+cos(α)
Final Result
Thus, the magnitude of the resultant force is:
R=√2F√1+cos(α)
---
We have two forces:
- Force 1: F
- Force 2: F
- Angle between them: α
The magnitude of the resultant R of two vectors can be calculated using the formula:
R=√F21+F22+2F1F2cos(α)
Since both forces are equal in magnitude, we can substitute F1=F and F2=F:
R=√F2+F2+2F⋅Fcos(α)
Combine the terms:
R=√F2+F2+2F2cos(α)=√2F2+2F2cos(α)
Factor out 2F2:
R=√2F2(1+cos(α))
Taking the square root of the factored expression gives:
R=√2F√1+cos(α)
Thus, the magnitude of the resultant force is:
R=√2F√1+cos(α)
Similar Questions
The greatest & the least magnitude of the resultant of two forces of constant magnitudes are P & Q respectively. If the forces act at an angle 2α, then prove that the magnitude of their resultant is given by √P2cos2α+Q2sin2α.
View SolutionThe resultant of two vectors at right angles is 5 N. If the angle between them is 120∘ and the resultant is √13 then the magnitude of vectors are
View SolutionTwo vectors, both equal in magnitude, have their resultant equal in magnitude of the either. Find the angle between the two vectors.
View SolutionTwo vectors of equal magnitude of 5 unit have an angle 600 between them. Find the magnitude of (a) the sum of the vectors and (b) the difference of the vectors.
 .
.  .
.
View SolutionTwo forces, each equal to F, act as shown in (figure) Their resultant is
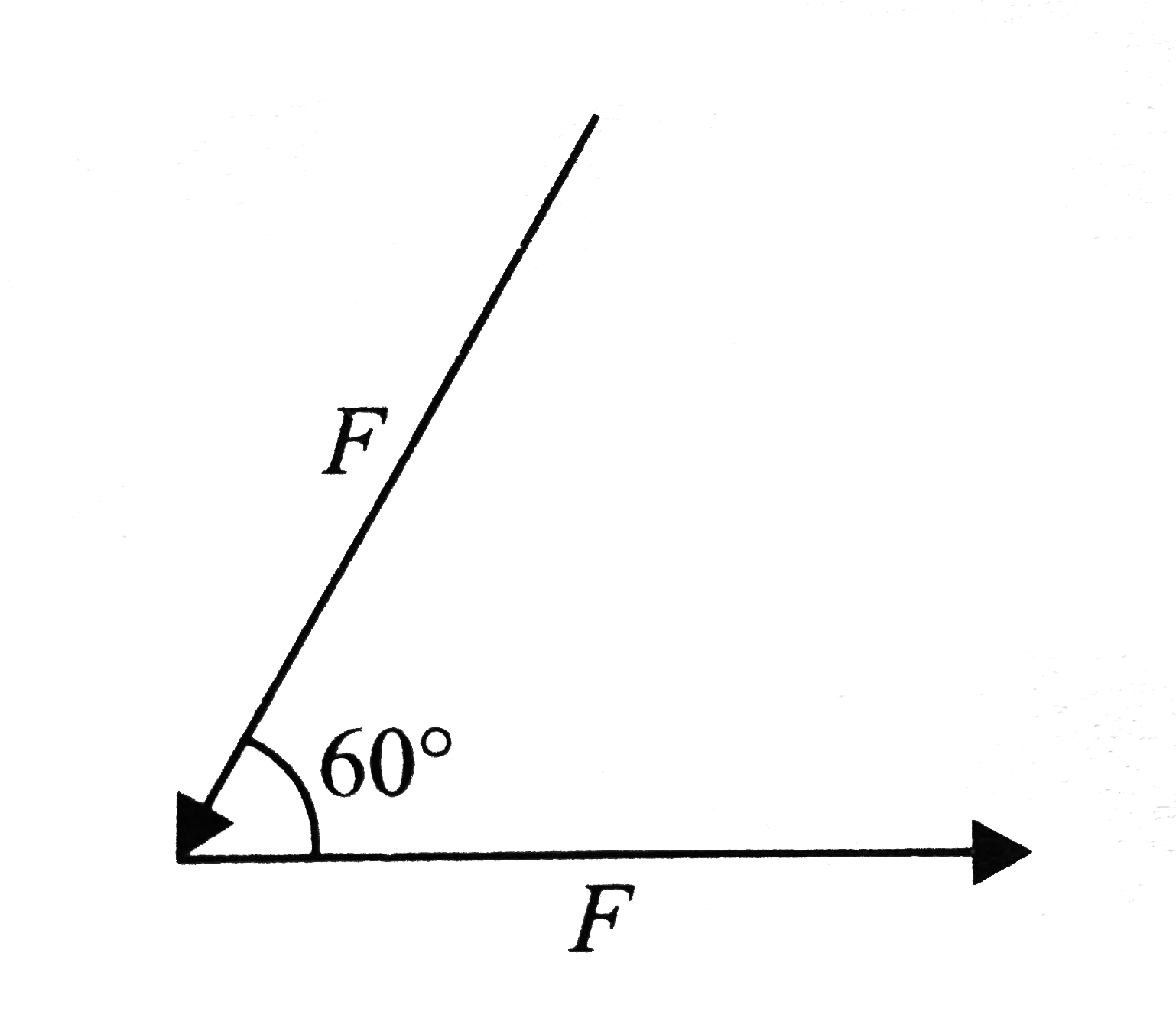
View SolutionTwo equal forces are acting at a point with an angle 60∘ between them. If the resultant force is equal to 4√3N, the magnitude of each force is
View SolutionTwo equal forces are acting at a point with an angle of 60∘ between them. If the resultant force is equal to 40√3N, The magnitude of each force is :-
View SolutionTwo vectors having equal magnitude of 5 units, have an angle of 60∘ between them. Find the magnitude of their resultant vector and its angle from one of the vectors.

View SolutionThe resultant of two forces has magnitude 20N. One of the forces is of magnitude 20√3N and makes an angle of 30∘ with the resultant. Then what is the magnitude of the other force?
View SolutionFive equal forces each of 20N are acting at a point in the same plane. If the angles between them are same, the resultant of these forces is
View Solution
