A river is flowing from west to east at a speed of 5 m per min. A man on the south bank of the river, capable of swimming at 10 m per min in still water, wants to swim across the river in the shortest time. He should swim in a direction
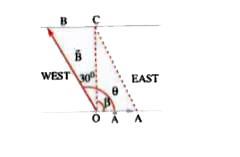
The situation is shown in fig.
OA=A, represents velocity of river which is 5mmt−1
OB=B , represents velocity of man in still water which is 10mmt−1
The man starts swimming from O and goes along OB to reach C by shortest possible path .
Here ,∠AOC=β=90∘
Here, A=5mmt−1,B=10mmt−1β=90∘,θ=?
From formula , tanβ=BsinθA+Bcosθ
putting values, we get ,tan90∘=10sinθ5+10cosθ=∞(∈f∈ite)
Hence, 5+10cosθ=0or10cosθ=−5
(or) cosθ=−0.5=cos120∘i.e.,θ=120∘
It makes ∠COB=30∘
The man should swim along OB which is 30∘ west of north .
Similar Questions
A river is flowing from west to east at a speed of 5 metres per minute.A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction.
View SolutionA river is flowing from west to east at a speed of 5 metres per minute.A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction.
View SolutionA river is flowing from west to east at a speed of 5metresperminute . A man on the south bank of the river , capable of swimming at 10metresperminute, in still water , wants to swim across the river in the shortest time . He should swim in a direction
View SolutionA river is flowing from west to east at a speed of 5m/s. A man on the south bank of the river capable of swimming at 10m/s in a still water wants to swim, across the river in a shortest time. He should swim in a direction
View SolutionA river is following from west to east at a speed of 5m/minute. A boy on the south bank of the river, capable of swimming at 10 meters/minute in still water, wants to swin across the river in the shortest time, (i) Find the direction in which he should swin, (ii) find the direction when drift along the river is zero.
View SolutionA river is flowing from east to west at a speed of 5mmin. A man on south bank of river, capable of swimming 10mmin ini still water, wants to swim across the river in shortest time. He should swim
View SolutionA river is flowing from the west to the east at 5m/min. A swimmer on the southerm bank can swim at 10 m/min in still water. In what direction should he swim if (i) He wishes to cross the river in minimum time (ii) He wishes to cross te river through shortest route
View SolutionA river is flowing from west to east with a speed of 5m/min. A man can swim in still water with a velocity 10m/min. In which direction should the man swim so as to take the shortest possible path to go to the south.
View SolutionA swimmer can swim in still water with a speed of 2.5 m/s. What is the shortest time taken by him to swim across the river?

View Solution
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. Suppose the boat wants to cross the river from A to the other side in the shortest possible time. Then what should be the direction of the velocity of boat relative to river?
View Solution
