If L=2.02m±0.01m,L2=1.02m±0.01m,determineL1+2L2.
To solve the problem of determining L1+2L2 given the measurements L1=2.02m±0.01m and L2=1.02m±0.01m, we will follow these steps:
Step 1: Identify the values and uncertainties
We have:
- L1=2.02m with an uncertainty of ΔL1=0.01m
- L2=1.02m with an uncertainty of ΔL2=0.01m
Step 2: Calculate 2L2
To find 2L2:
2L2=2×1.02m=2.04m
Step 3: Determine the uncertainty in 2L2
The uncertainty in 2L2 is calculated by multiplying the uncertainty of L2 by 2:
Δ(2L2)=2×ΔL2=2×0.01m=0.02m
Step 4: Add L1 and 2L2
Now, we can add L1 and 2L2:
L1+2L2=2.02m+2.04m=4.06m
Step 5: Calculate the total uncertainty
When adding quantities, the total uncertainty is the sum of the individual uncertainties:
Δ(L1+2L2)=ΔL1+Δ(2L2)=0.01m+0.02m=0.03m
Final Result
Thus, the final result for L1+2L2 is:
L1+2L2=4.06m±0.03m
---
We have:
- L1=2.02m with an uncertainty of ΔL1=0.01m
- L2=1.02m with an uncertainty of ΔL2=0.01m
To find 2L2:
2L2=2×1.02m=2.04m
The uncertainty in 2L2 is calculated by multiplying the uncertainty of L2 by 2:
Δ(2L2)=2×ΔL2=2×0.01m=0.02m
Now, we can add L1 and 2L2:
L1+2L2=2.02m+2.04m=4.06m
When adding quantities, the total uncertainty is the sum of the individual uncertainties:
Δ(L1+2L2)=ΔL1+Δ(2L2)=0.01m+0.02m=0.03m
Thus, the final result for L1+2L2 is:
L1+2L2=4.06m±0.03m
Similar Questions
If L1=2.02m±0.01m,L2=1.02m±0.01m, determine L1+2L2
View SolutionIf L=(20±0.01)mandB=(10±0.02)m then L/B is
View SolutionIf L=20.04m±0.01m,B=2.52m±0.02m. The value of (L×B) is
View SolutionIf L=(2±0.01)mandB=(1±0.02)m then L/B is
View SolutionIf L = 20.04 m ±0.01 m , B= 2.52 m ± 0.02 m . What are the values of (L×B)and(L+B) ?
View SolutionIf L = 20.04 m ±0.01 m , B= 2.52 m ± 0.02 m . What are the values of (L×B)and(L+B) ?
View SolutionIf L = 2.01 m ± 0.01 m , what is 3 L ?
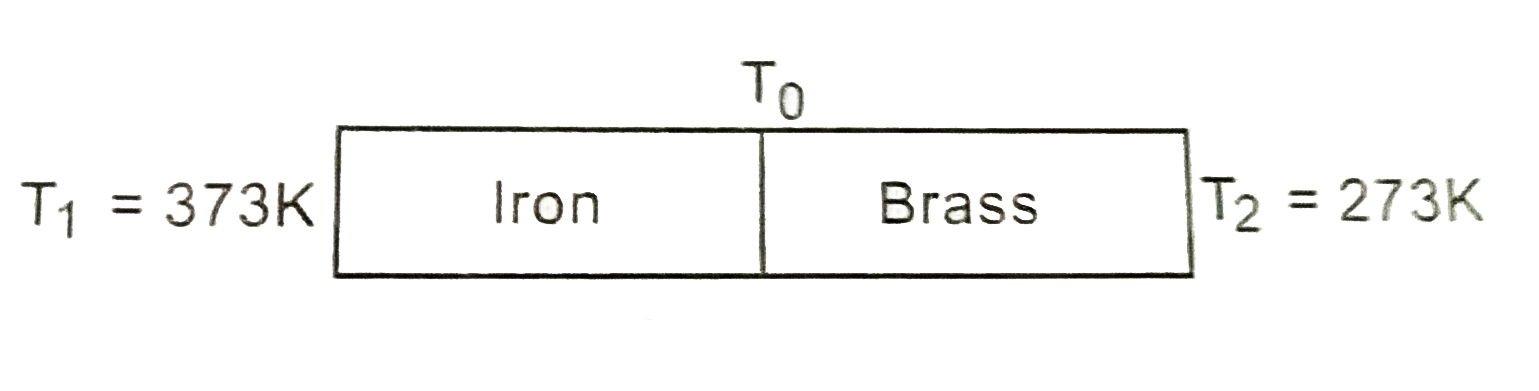
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
View SolutionThe quantum number of electrons are given below: Arrange then in order of increasing energies
a.n=4,l=2,m1=−2,ms=−12
b.n=3,l=2,m1=1,ms=+12
c.n=4,l=1,m1=0,ms=+12
e.n=3,l=2,m1=−2,ms=+12
f.n=4,l=1,m1=+1,ms=+12
View Solution

